- 「行列」について学びたいけど理解できるか不安・・・
- 「行列」についてどこから学んでいいか分からない?
- 「行列」を体系的に教えて!
「行列」は人工知能(AI)を含む機械学習において用いられれている重要なものですが、興味があっても難しそうで何から学んだらよいか分からず、勉強のやる気を失うケースは非常に多いです。
私は過去に基本情報技術者試験(旧:第二種情報処理技術者試験)に合格し、また2年程前に「一般社団法人 日本ディープラーニング協会」が主催の「G検定試験」に合格しました。現在、「E資格」にチャレンジ中ですが3回不合格になり、この経験から学習の要点について学ぶ機会がありました。
そこでこの記事では、「行列」についてポイントを解説します。
この記事を参考にして「行列」が理解できれば、E資格に合格できるはずです。
目次
行列とは
スカラーとベクトルの違い
| スカラー | ベクトル |
|---|---|
| ・だいたい、いわゆる普通の数 | ・「大きさ」と「向き」を持つ |
| ・+-×÷の演算が可能 | ・矢印で図示される |
| ・ベクトルに対する係数になれる | ・スカラーのセットで表示される |
行列
行列とは・・・
- スカラーを表にしたもの
- ベクトルを並べたもの
(ベクトルのベクトル)

学生
行列って何に使うの?

著者
行列は次のことに使えるよ!
・ベクトルの変換
・連立方程式を解く
連立1次方程式
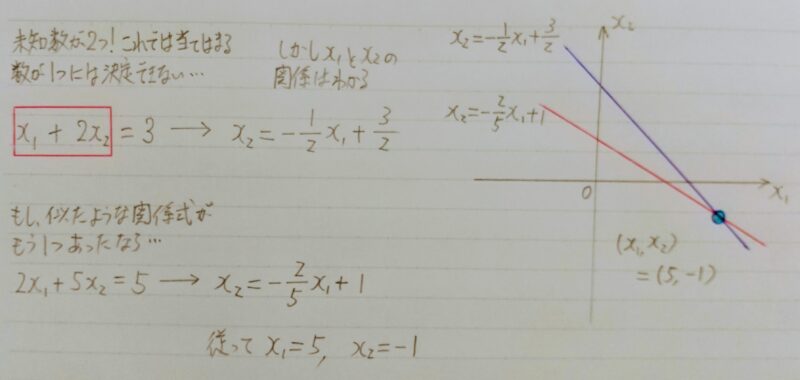
行列を用いた表示
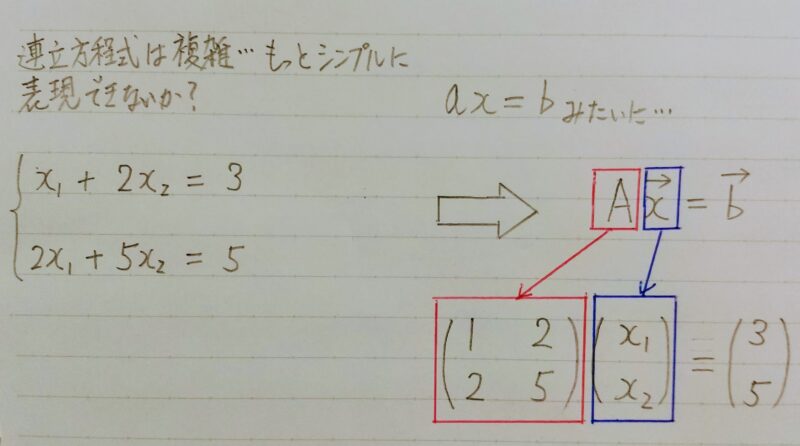
※この係数をまとめて「表」のようにした部分を「行列」と呼ぶ
行列とベクトルの積
- 例題
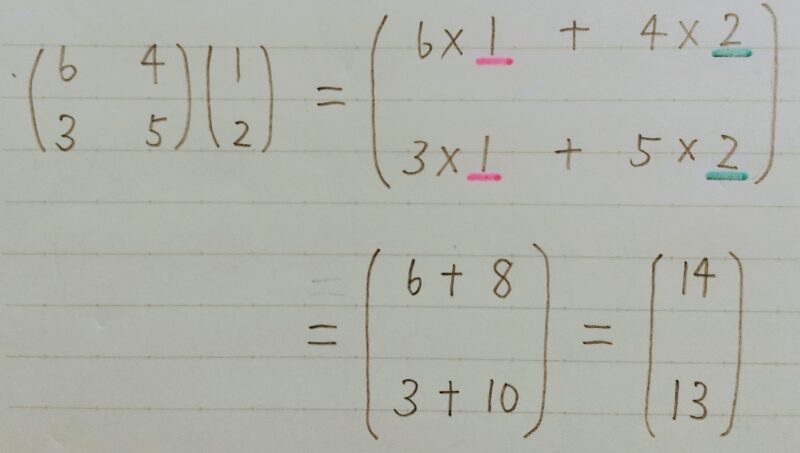
行列とベクトルの計算手順
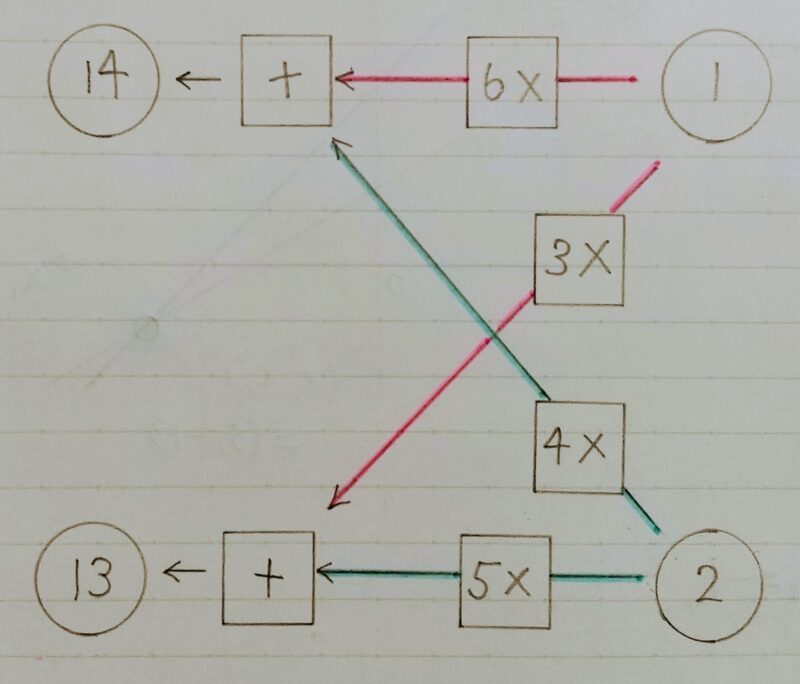
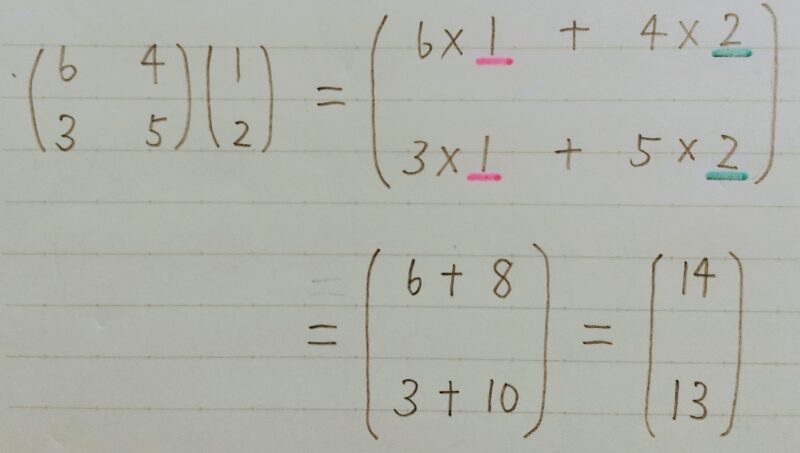
変換後の要素のある「ひとつ」は元の要素の「すべて」から影響を受けている
行列の積

「行」×「列」で新たな行列の成分を求める!
行列の積 例題
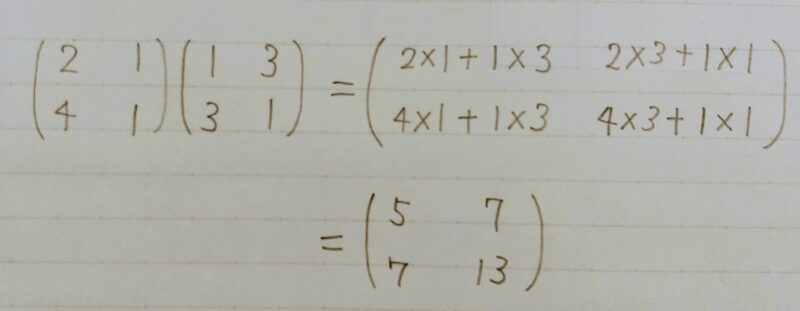
逆行列とは
連立1次方程式の解き方
別記事『【日常生活で使える数学】行列の便利さを徹底解説!』を参照
行列の「逆数」のようなもの
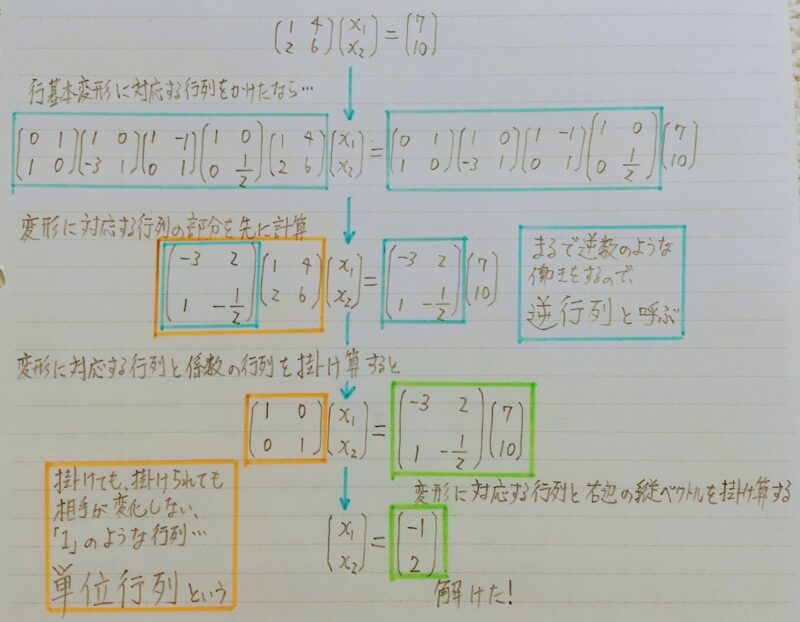
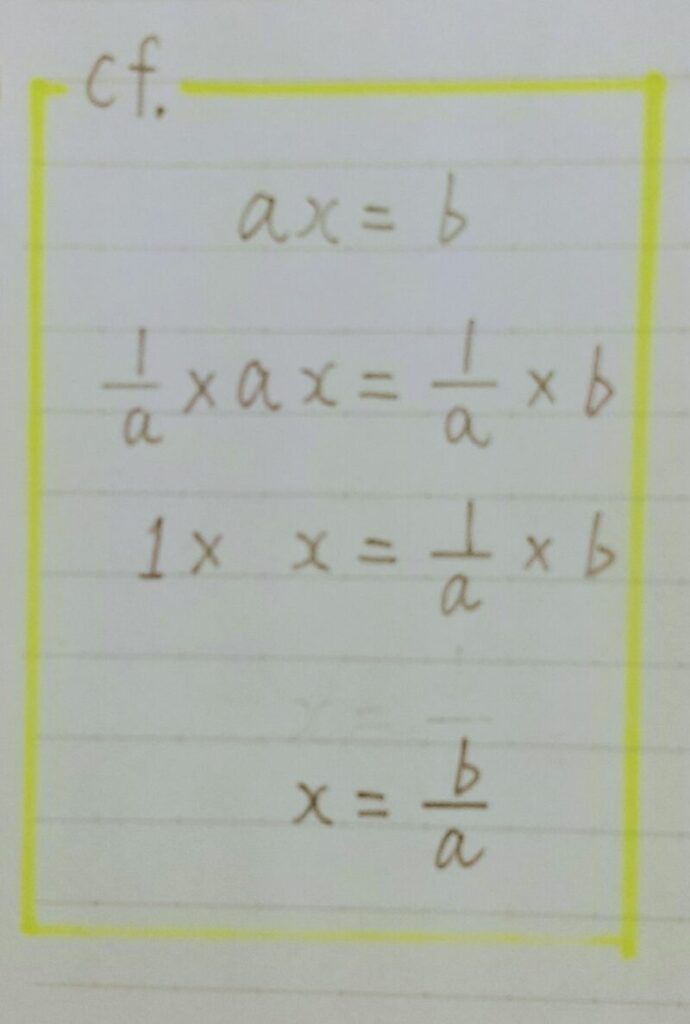
単位行列と逆行列

逆行列の求め方

逆行列を求める問題

逆行列が存在しない条件
逆数が存在しない数があるのと同様に逆行列が存在しない行列というものもある
↓
解がない、解が1組に定まらないタイプの連立方程式
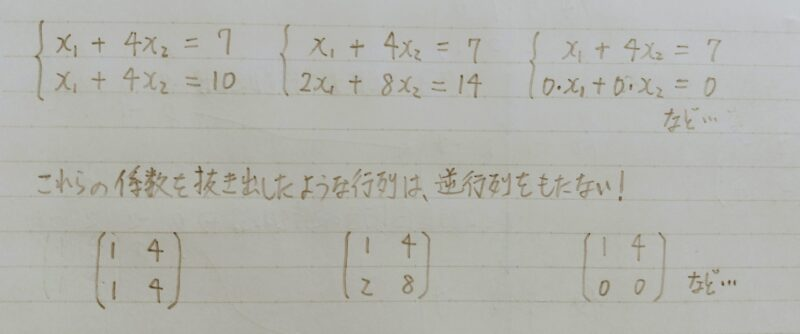
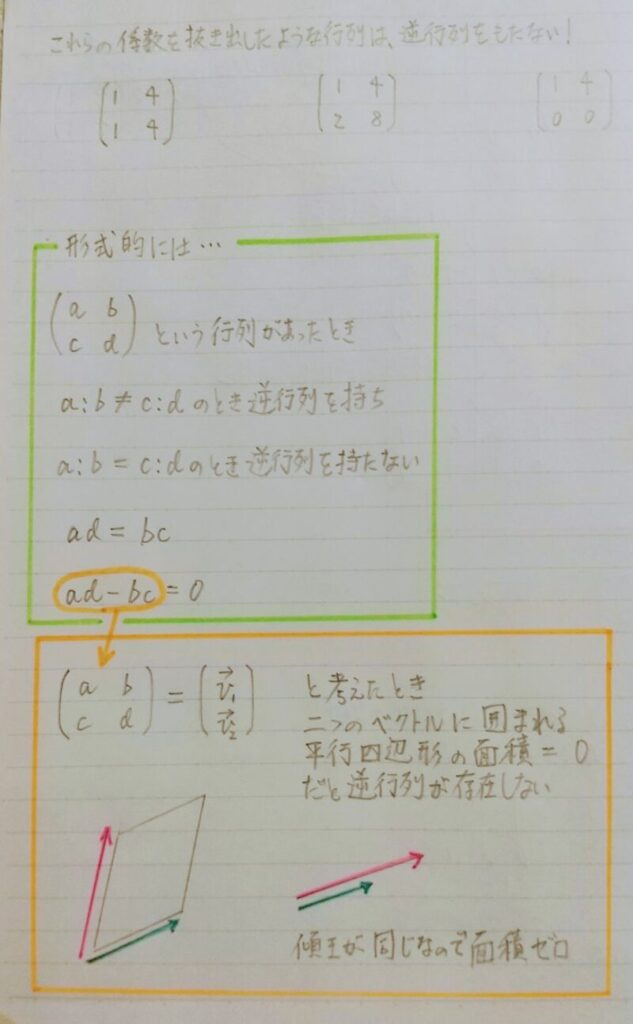
行列式とは
行列式の特徴
ある行列が2つの横ベクトルの組み合わせだと考えたとき


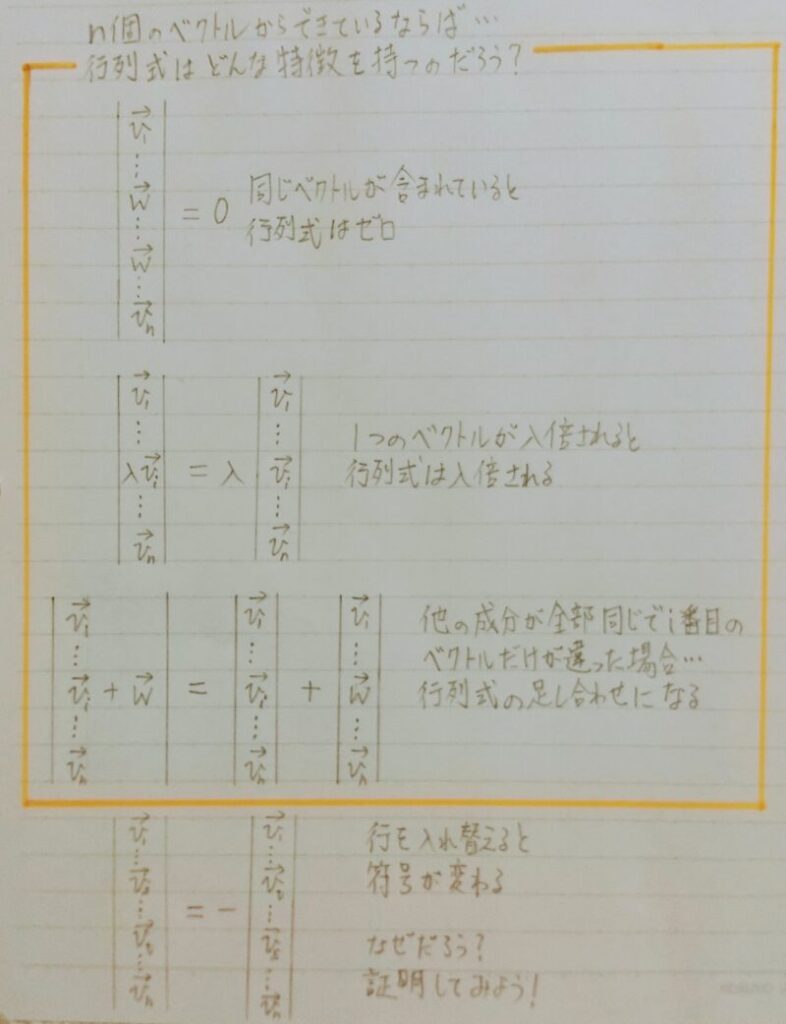
問題
問題 解答
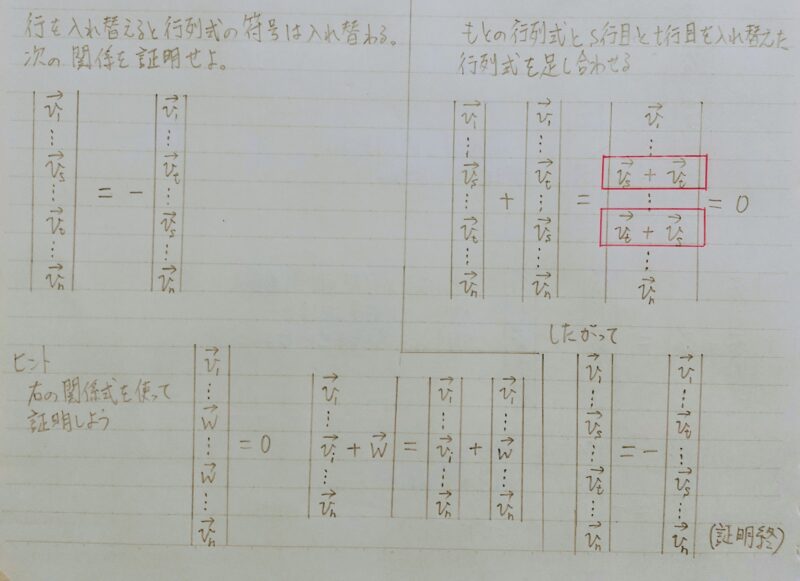
行列式の求め方

行列式を求める問題
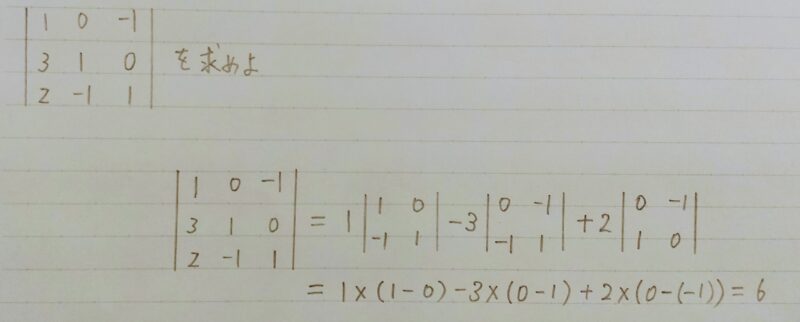
まとめ
最後まで読んで頂きありがとうございます。
皆様のキャリアアップを応援しています!!

コメント