【E資格不合格から学ぶ】LSTM（Long Short Term Memory）のポイントを解説！

2023年10月10日2024年12月18日

「LSTM（Long Short Term Memory）」について学びたいけど理解できるか不安･･･
「LSTM（Long Short Term Memory）」についてどこから学んでいいか分からない？
「LSTM（Long Short Term Memory）」を体系的に教えて！

　「LSTM（Long Short Term Memory）：長短期記憶」は、RNN（再帰型ニューラルネットワーク）の課題（勾配消失問題）を構造を変えて解決した画期的なニューラルネットワークのことです。ここで興味があっても難しそうで何から学んだらよいか分からず、勉強のやる気を失うケースは非常に多いです。

　私は過去に基本情報技術者試験（旧：第二種情報処理技術者試験）に合格し、また2年程前に「一般社団法人日本ディープラーニング協会」が主催の「G検定試験」に合格しました。現在、「E資格」にチャレンジ中ですが３回不合格になり、この経験から学習の要点について学ぶ機会がありました。

　そこでこの記事では、「LSTM」を学習する際のポイントについて解説します。

　この記事を参考にして「LSTM」のポイントが理解できれば、E資格に合格できるはずです。

<<「LSTM」のポイントを今すぐ見たい方はこちら

1.LSTM（Long Short Term Memory）の概要

RNN（再起型ニューラルネットワーク）の課題

時系列を遡れば遡るほど、勾配が消失 → 長い時系列の学習が困難

↓

課題の解決策

勾配消失の解決方法とは別で、構造自体を変えて解決したものがLSTM

勾配消失問題とは

　誤差逆伝搬法が下位層に進んでいくに連れて、勾配がどんどん緩やかになっていく。そのため、勾配降下法による更新では下位層のパラメータはほとんど変わらず、訓練は最適値に収束しなくなる。

勾配爆発とは･･･

勾配が、層を逆伝播するごとに指数関数的に大きくなっていく。

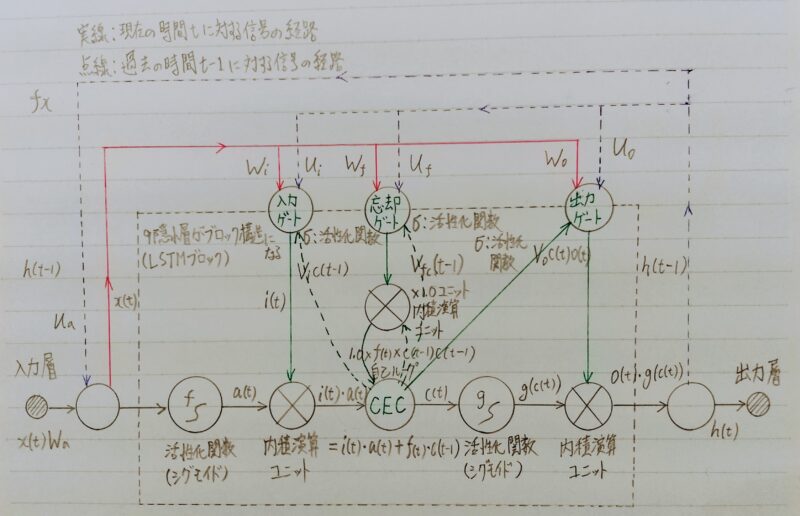
LSTMモデルの定式化

LSTMの特徴

上図のLSTMは、従来のRNNの欠点である長期依存性の学習の困難さを克服するため、長期にわたる過去情報を記憶するための仕組みを備えている。
役割の異なる３つのゲート（入力ゲート、出力ゲート、忘却ゲート）を備えている。
LSTM：長期記憶（long term memory）と短期記憶（short term memory）という意味。

Pythonコード

LSTMのコードに使用される関数を以下に挙げる。

np.random.randn関数：
標準正規分布の乱数を生成
例）np.random.randn(4,4) ← 標準正規分布の4×4の行列
np.concatenate関数：
2個以上の配列を軸指定して連結できる。

1.1 CEC（Constant Error Carousel）

CEC（Constant Error Carousel）とは･･･

RNNの中間層
勾配消失および勾配爆発の解決方法として、勾配が１であれば解決できる。

特徴

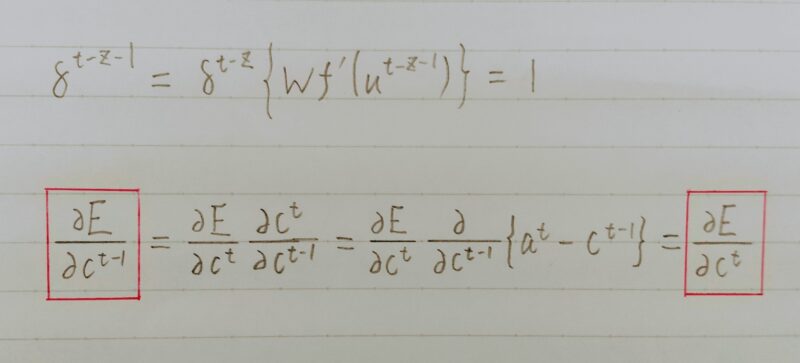
CECとは誤差が消失しないようにするニューロンのこと。
入力ゲートおよび出力ゲートは時間依存性があるデータを受け取ったときのみ活性化を起こすための仕組みである。
過去の値を必要な時のみ取り出すことができる。

CECの課題とは･･･

入力データについて、時間依存度に関係なく重みが一律である。
⇒　ニューラルネットワークの学習特性が無い

入力層→隠れ層への重み　　　隠れ層→出力層への重み
　　入力重み衝突　　　　　　　　出力重み衝突

確認テスト
Q．LSTMとCECが抱える問題とは何か？
A．LSTMは計算量が膨大。
CECは学習機能がない。

1.2 入力ゲートと出力ゲート

入力・出力ゲートの役割とは･･･

入力・出力ゲートを追加することで、それぞれのゲートへの入力値の重みを、
重み行列W,Uで可変可能とする。
↓
CECの課題を解決

1.3 忘却ゲート

忘却ゲートとは･･･

LSTMの現状

CECは、過去の情報が全て保管されている。

課題

過去の情報が要らなくなった場合、削除することはできず、保管され続ける。

解決策

過去の情報が要らなくなった場合、そのタイミングで情報を忘却する機能が必要。
↓
　忘却ゲートの誕生

1.4 覗き穴結合

覗き穴結合とは･･･

CECの課題

CECの保存されている過去の情報を、任意のタイミングで他のノードに伝播させたり、あるいは任意のタイミングで忘却させたい。
CEC自身の値は、ゲート制御に影響を与えていない。

解決策

CEC自身の値に、重み行列を介して伝播可能にした構造とする。
⇒　覗き穴（peep hole）結合という。

覗き穴結合の仕組み

出力ゲートの計算式について従来のものと覗き穴結合を使用した場合を比較する。
〈従来の場合〉
　o_t＝σ（x_tW₀＋h_t-1U₀　　　　＋b₀）
〈覗き穴結合を使用した場合〉
　o_t＝σ（x_tW₀＋h_t-1U₀＋c_t⦿V₀＋b₀）

　o_t：出力ゲート
　x_t：入力
　W：x_t（入力）に対する重み
　h_t-1：前時刻の中間層出力
　U：前時刻の中間層出力に対する重み
　V：CECの状態cに対する重み
　b：バイアス
　σ：シグモイド関数

　※ c_t⦿V₀･･･c_t、V₀のアダマール積

アダマール積（英: Hadamard product）は、同じサイズの行列に対して成分ごとに積を取ることによって定まる行列の積である。
引用元：Wikipedia

アダマール積を用いるメリット
通常の行列積の演算より演算速度を改善。

2.GRU（Gated Recurrent Unit）

2.1 概要

GRUとは･･･

LSTMの課題

パラメータ数が多く、計算負荷が高くなる。

解決策

パラメータを大幅に削減し、精度はLSTMと同等またはそれ以上が望めるようになった構造。⇒ GRU（Gated Recurrent Unit）
補足）Gated Recurrent Unit：ゲート型再帰ユニット

メリット

計算負荷が低い。

2.2 全体像

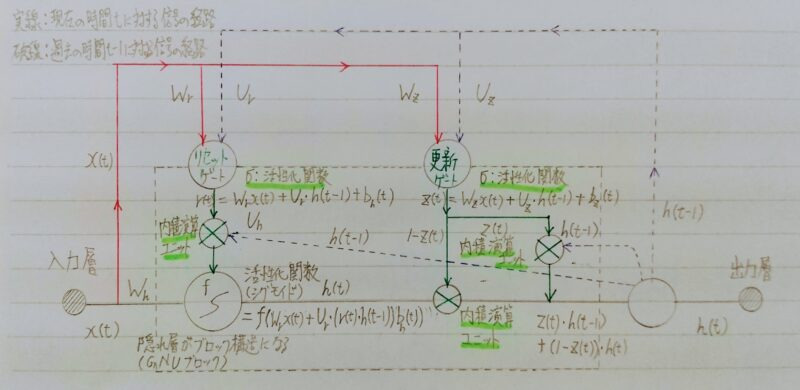
GRUの全体像

特徴

記憶セルを持たず２つのゲート（更新ゲート・リセットゲート）を持つ
新しい中間状態＝1ステップ前の中間表現＋計算された中間表現

2.3 確認テスト

◎確認テスト
Q．LSTMとGRUの違いを簡潔に述べよ。
A．パラメータの数が違う。

◎確認テスト
Ｑ．GRU（Gated Recurrent Unit）もLSTMと同様にRNNの一種であり、単純なRNNにおいて問題となる勾配消失問題を解決し、長期的な依存関係を学習することができる。LSTMに比べ変数の数やゲートの数が少なく、より単純なモデルであるが、タスクによってはLSTMより良い性能を発揮する。以下のプログラムはGRUの順伝播をおこなうプログラムである。ただし_sigmoid関数は要素ごとにシグモイド関数を作用させる関数である。 (こ)にあてはまるものはどれか。

　def gru(x, h, W_r, U_r, W_z, U_z, W, U):
“””
　　　x: inputs, (batch_size, input_size)
  　　 h: outputs at the previous time step, (batch_size, state_size)
　　　↑前時刻の隠れ層での出力
    　 W_r, U_r: weights for reset gate
    　 W_z, U_z: weights for update gate
    　 U, W: weights for new state
    　 “””
    　　# ゲートを計算
　　　 r = _sigmoid(x.dot(W_r.T) + h.dot(U_r.T))
    　　 z = _sigmoid(x.dot(W_z.T) + h.dot(U_z.T))

　　　 # 次状態を計算
　　　 h_bar = np.tanh(x.dot(W.T) + r * h).dot(U.T))
　　　 ↑新しい隠れ状態での出力
　　　 h_new =（こ）
　　　 return h_new
Ａ．(1-z)*h + z*h_bar