- 機械学習には興味があるけど「情報科学」が理解できるか不安・・・
- 「情報科学」についてどこから学んでいいか分からない?
- 「情報科学」を体系的に教えて!
「情報科学」は機械学習(深層学習を含む)において用いられれている重要なものですが、興味があっても難しそうで何から学んだらよいか分からず、勉強のやる気を失うケースは非常に多いです。
私は過去に基本情報技術者試験(旧:第二種情報処理技術者試験)に合格し、また2年程前に「一般社団法人 日本ディープラーニング協会」が主催の「G検定試験」に合格しました。現在、「E資格」にチャレンジ中ですが3回不合格になり、この経験から学習の要点について学ぶ機会がありました。
そこでこの記事では、「情報科学」のうち「交差エントロピー」や「相互情報量」等についてポイントを解説します。
この記事を参考にして「情報科学」が理解できれば、E資格に合格できるはずです。
情報量
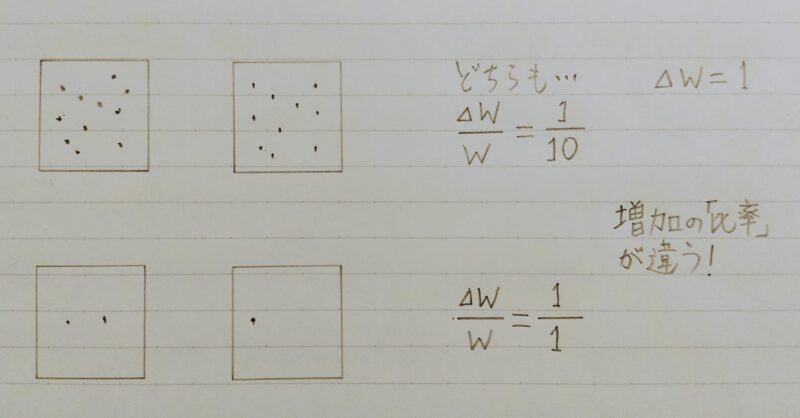

増えた情報量は同じなのに、何が違うの?

増加の「比率」が違うよ!!
自己情報量
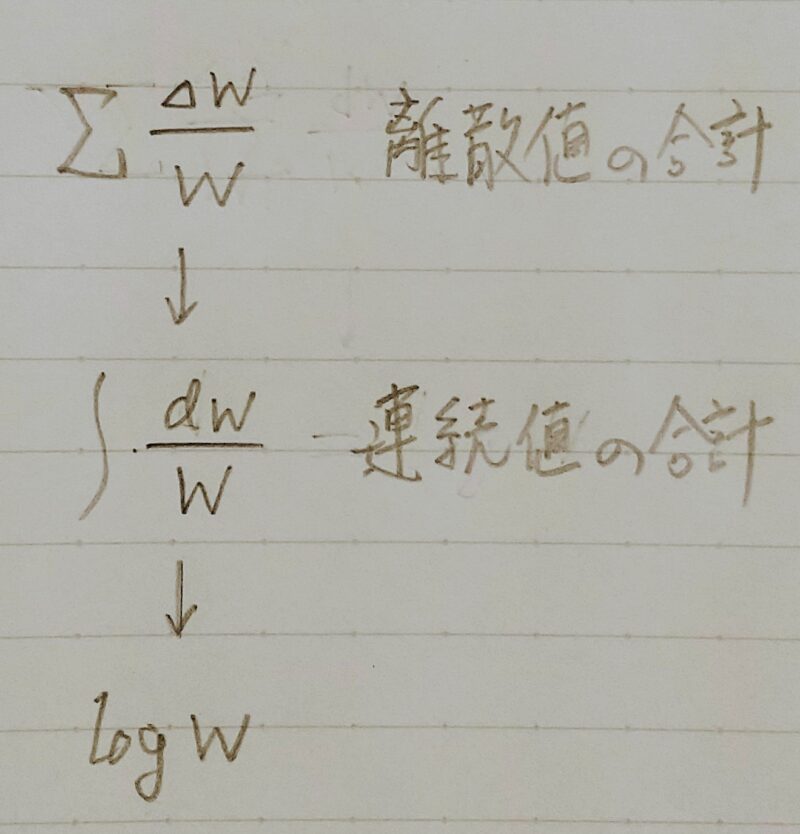
I(x)= ーloga(P(x))
= loga(W(x))
I(x):自己情報量
P(x):確率
W(x):全情報量
P(x)=1/W(x) ← P(x)とW(x)の関係
- 対数の底(a)が2のとき、単位はビット(bit)
- 対数の底(a)がネイピア(=自然対数の底)eのとき、単位は(nat)

なぜ、自己情報量はわざわざ確率P(x)の対数をとるのかな?

2つあるよ!!
- ①確率P(x)が小さくなるほど自己情報量I(x)を大きくしたいから(確率が小さい(=より珍しい情報=より価値のある情報)ほど自己情報量は大きいと考えるよ)
- ②自己情報量I(x)を求める計算を楽にしたいから(対数にすると計算が足し算になるよ)
シャノンエントロピー
- 単に「エントロピー」ともいう
- 微分エントロピーともいうが、微分しているわけではない。
(differentialの誤訳か?) - 自己情報量の期待値 ← 情報の珍しさ(=情報の価値が大きさ)の平均値のようなもの
- H(x) = E(I(x))
=ーE(log(P(x)))
=ーΣ(P(x)log(P(x)))
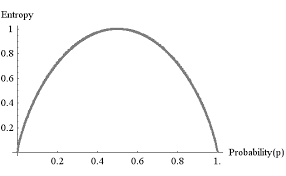
(コイン投げの場合)

上のグラフはどういう意味があるの?

コインの表と裏の出る確率が、
表が出る確率が50%(=0.5)
裏が出る確率が50%(=0.5)
のとき、表が出た情報に最も価値がある(=現実に最も近い情報)といえるよ!!

じゃコインが表の出る確率が100%のとき表が出たという情報に価値はないの?

100%表の出るコインで表が出ても
その情報は珍しくないから情報に価値はない(=現実と合っていない)と考えるよ!!

シャノンエントロピーは何の役に立つの?

シャノンエントロピーで現実を予想できるよ。
機械学習において、シャノンエントロピーを最大にするよう誤差関数に組み込むことで現実を予想できるかもしれないよ!!
KLーダイバージェンス
- KLーダイバージェンス(Kullback-Leibler divergence)
KullbackとLeiblerは人名 - 同じ事象・確率変数における異なる確率分布P,Qの違いを表す

カルバック・ライブラー ダイバージェンスは確率分布P、Qの違いを表す距離みたいなもの?

距離と似ているけど距離ではないんだよ!!
なぜなら、KLーダイバージェンスの式は二つの確率分布の順番を入れ替えると式の値が変わるからだよ!
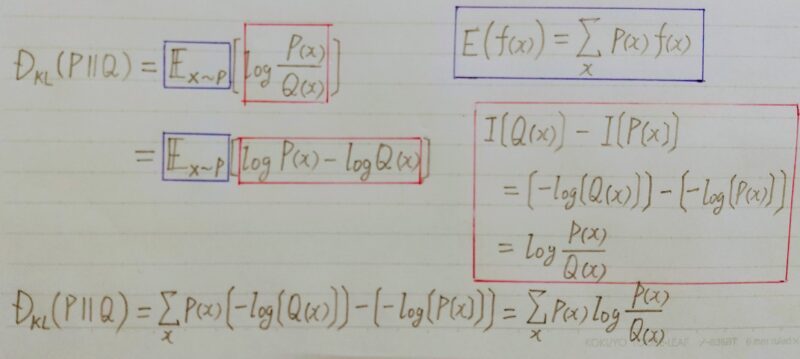
DKL(P||Q):カルバック・ライブラー ダイバージェンスとは古い確率分布Qが分かった後、起こった新しい確率分布Pから眺めた時にどれくらい情報が違うかを示したもの
P:Qの後に起こった確率分布
Q:Pの前に分かった確率分布
Q.比較する二つの確率分布が同じとき、KLーダイバージェンスの値はいくつになるか?
A.log(P(x)/Q(x))=log(1)=0になるから0
VAE(変分オートエンコーダー)においてKLーダイバージェンスを正則化項として加える。
JSーダイバージェンス
- KLーダイバージェンスの式は二つの確率分布の順番を入れ替えると式の値が変わるため、JSーダイバージェンスの式が用いれらることがある。
- 応用例)
GAN(画像認識&画像生成)のDiscriminatorにおいて2つの確率分布がどれくらい近いかを判定するために使用
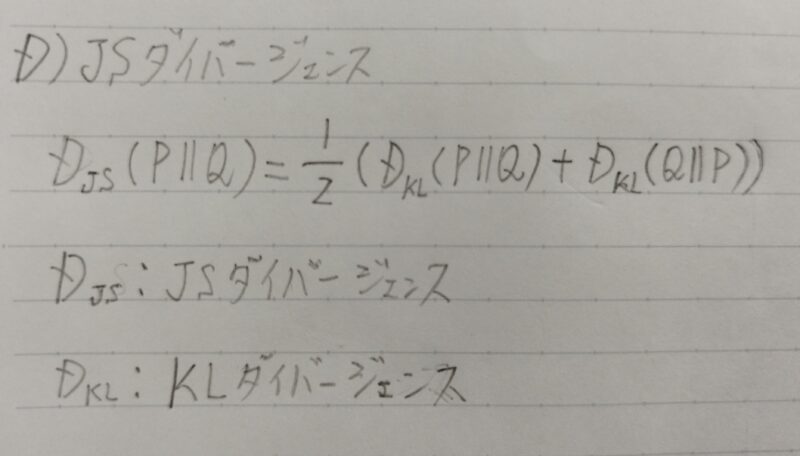
JSーダイバージェンスは二つの確率分布を入れ替えても対称性が成り立つ。
引用元:「VasteeLab」
様々なエントロピー
交差エントロピー
- カルバック・ライブラー ダイバージェンスの一部分を取り出したもの
- Qについての自己情報量をPの分布で平均している
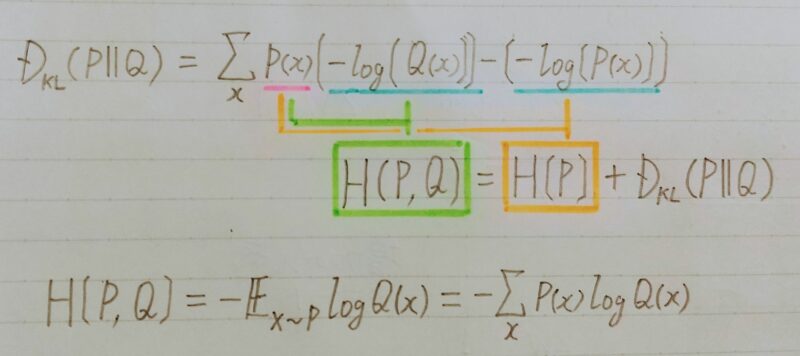
- DKL(P||Q):カルバック・ライブラー ダイバージェンスとは古い確率分布Qが分かった後、起こった新しい確率分布Pから眺めた時にどれくらい情報が違うかを示したもの
- H(P,Q):logQ(x)をPで平均したもの
結合エントロピー

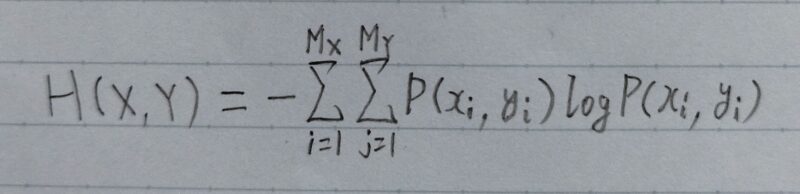
P(xi,yi):xiとyiが同時に起こる確率
logの底は2
Q.ある商店で、1時間に80人の客が来店した。来店した客の性別の内訳と、客が眼鏡をしているかの内訳は以下のとおりであった。
| 男 | 女 | 合計 | |
|---|---|---|---|
| 眼鏡有 | 10人 | 10人 | 20人 |
| 眼鏡無 | 40人 | 20人 | 60人 |
| 合計 | 50人 | 30人 | 80人 |
この時に来店した客の性別と、その客が眼鏡をしているかを知った時の同時エントロピー(結合エントロピー)の値を求めよ。
A.同時エントロピーは定義式は以下のとおりである。
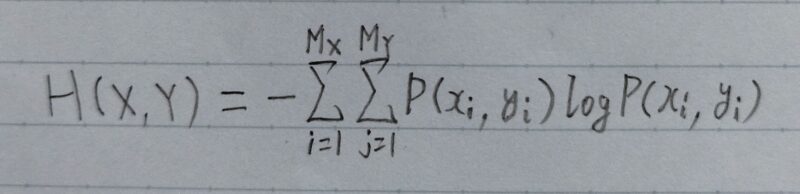
P(xi,yi)は「xiとyiが同時に起こる確率」であるから、次のように整理する。
x1:男
x2:女
y1:眼鏡有
y2:眼鏡無
H(X,Y)=ーP(x1,y1)log2(P(x1,y1))-P(x1,y2)log2(P(x1,y2))
-P(x2,y1)log2(P(x2,y1))-P(x2,y2)log2(P(x2,y2)) ・・・①
P(x1,y1)=10/80=1/8 ・・・②
P(x1,y2)=40/80=1/2 ・・・③
P(x2,y1)=10/80=1/8 ・・・④
P(x2,y2)=20/80=1/4 ・・・⑤
②,③,④,⑤を①へ代入すると
H(X,Y)=-(1/8)log2(1/8)-(1/2)log2(1/2)
-(1/8)log2(1/8)-(1/4)log2(1/4)

上記の計算は計算機じゃないとできないかな?

実は次のように計算すると手計算でも解けるよ!
H(X,Y)=-(2/8)log2(1/8)-(1/2)log2(1/2)
-(1/4)log2(1/4)

ここでlogの公式を思い出してほしい!
logab/c=logab-logac
H(X,Y) =-(2/8){log21-log28}-(1/2){log21-log22}
-(1/4){log21-log24}

ここでlog2は次の値になるよ
log21=0
log22=1
log24=2
log28=3
H(X,Y) =-(2/8)×(0-3)-(1/2)×(0-1)
-(1/4)×(0-2)
=6/8+4/8+4/8
=1.75
条件付きエントロピー

コインを2回投げる。1回目には表が出る確率1/2、裏が出る確率1/2のコインを投げる。2回目にはほぼ必ず裏が出るコインを投げる。表を1、裏を0として各回の表裏を表す確率変数をX、Yとする。
条件付きエントロピーH(Y|X)を求めよ。
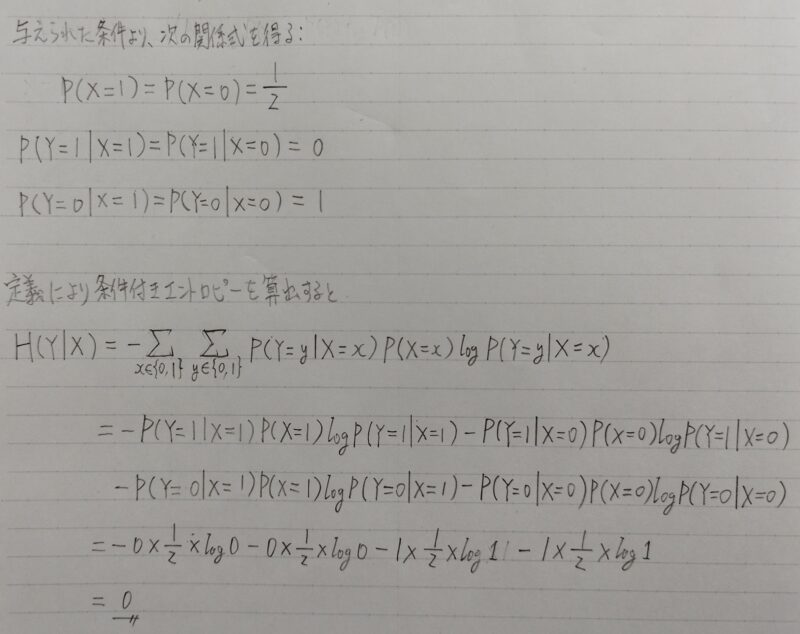

上記の解答は次のように解釈できるよ!
「2回目にほぼ必ず裏が出る」ということは、Xの出た目に関係なくYの情報量は「0」なんだ。だから「Xの目が表か裏か知った」としてもYの情報量には影響ないんだよ!
相互情報量
- 相互情報量(mutual information)(=伝達情報量(transinformation)):
2つの確率変数の相互依存度の尺度を表す量。不確実性(情報エントロピー)の減少量とみなせる。

上式より、相互情報量はXとYについて対称。
以下の2つの理由により、相互情報量は、XとYの「依存度」を表す指標と考えることができる。
理由1:XとYが独立のとき、I(X;Y)=0となる。そして、I(X;Y)の最小値は0である。つまりXとYがある意味で最も依存していないときに、相互情報量は最小となる。
理由2:Xの分布を固定してI(X;Y)の取りうる値について考える。このとき、Yの分布がXの分布と同じである場合に、I(X;Y)は最大値を達成する。つまりXとYが最も依存しているときに、相互情報量は最大となる。
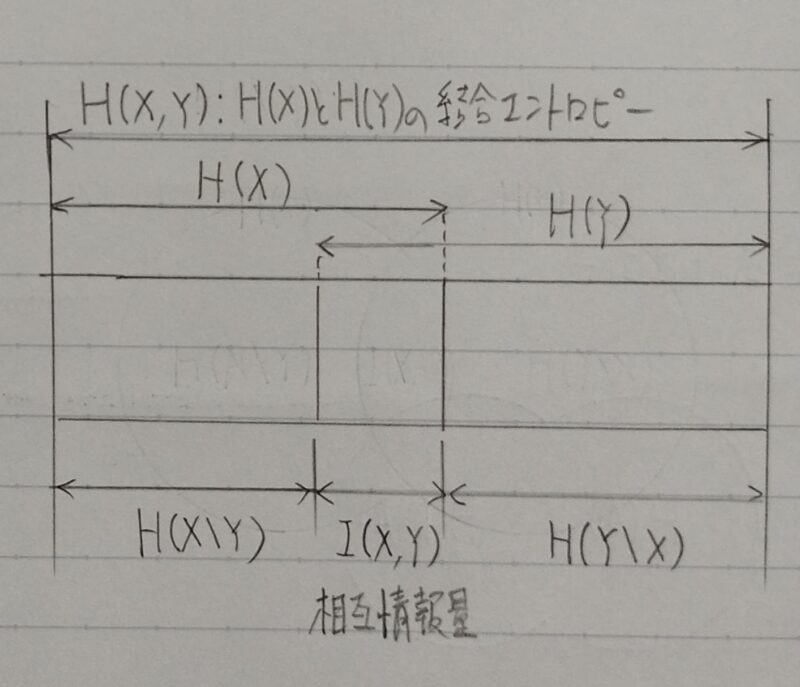
I(X,Y)=H(X)ーH(X|Y)
=H(Y)ーH(Y|X)
=H(X)+H(Y)ーH(X,Y)
I(X,Y):確率変数X,Yの相互情報量
H(X):確率変数Xのエントロピー
H(Y):確率変数Yのエントロピー
H(X,Y):確率変数X,Yの結合エントロピー
H(X|Y):Yが分かった後のXのエントロピー
H(Y|X):Xが分かった後のYのエントロピー
「XとYの依存度」は「Xのあいまいさ」と「Yを知ったもとでのXのあいまいさ」の差である。
コインを2回投げる。1回目には表が出る確率1/2、裏が出る確率1/2のコインを投げる。2回目にはほぼ必ず裏が出るコインを投げる。表を1、裏を0として各回の表裏を表す確率変数をX,Yとする。
相互情報量I(X;Y)を求めよ。
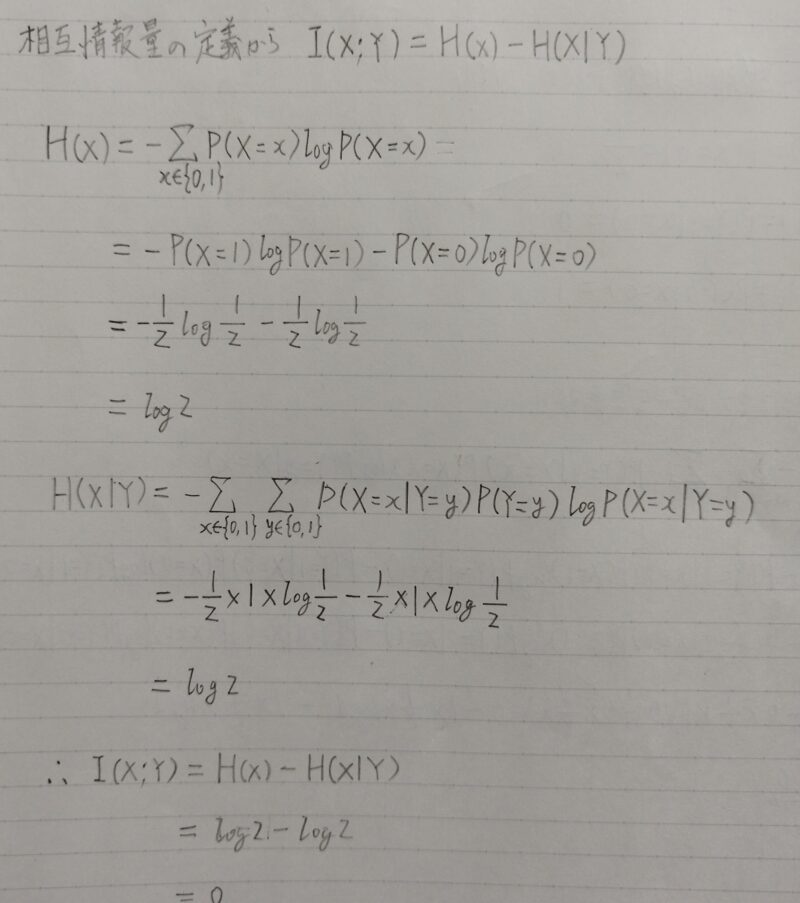

上記の解答は別の解答もできるよ!
相互情報量は次の式でも表現できる。
I(X;Y)=H(Y)ーH(Y|X)
H(Y)=0 ← 2回目にほぼ必ず裏が出る
H(Y|X)=0 ← 条件付きエントロピーの例題解答参照
ゆえにI(X;Y)=0ー0=0
つまり、「Xの目が表であるか裏であるかという情報」と「Yの出る目の情報」には関係性はない。なぜなら「2回目にほぼ必ず裏が出る」からだよ!
まとめ
- 自己情報量・シャノンエントロピーの定義
・自己情報量:ーlogP(E)
・シャノンエントロピー(=平均情報量=情報エントロピー)
事象Xが起こる確率をP(X)とする。ある事象Xが起こったとわかった時に得られ「情報量の期待値」をシャノンエントロピー(=平均情報量=情報エントロピーという。
H=ーΣP(E)logP(E)エントロピー(シャノンエントロピー)
H(x) =ーΣ(P(x)log(P(x))) - 結合エントロピー
H(X,Y)=ーΣΣP(X,Y)logP(X,Y)
H(X,Y)=H(X)+H(Y|X)
=H(Y)+H(X|Y) - 条件付きエントロピー
H(Y|X)=H(X,Y)ーH(X)
H(X|Y)=H(X,Y)ーH(Y) - KLダイバージェンス・交差エントロピー
・カルバック・ライブラーダイバージェンス(Kullback–Leibler divergence)二つの確率分布の擬距離を定量化する指標
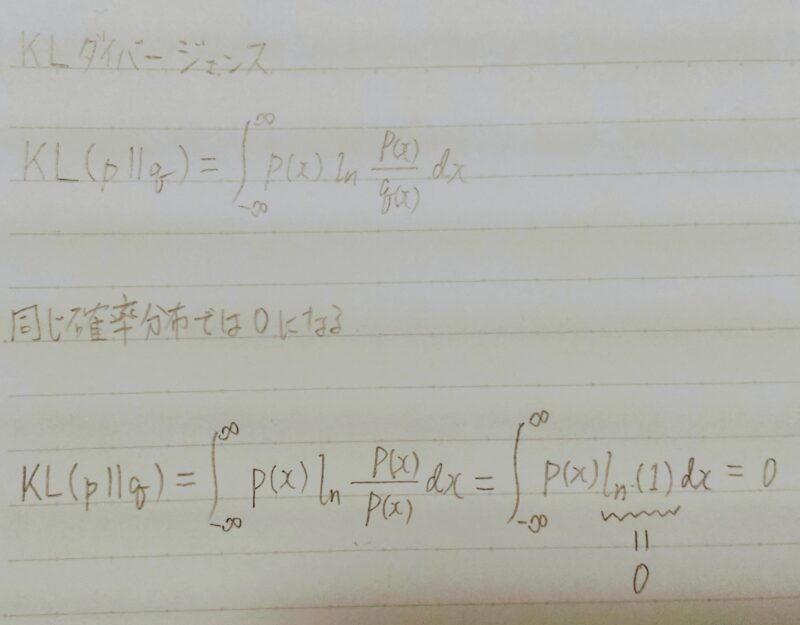
【特性】
①比較する確率分布が同じ場合は0になる。
②常に0を含む正の値となり、確率分布が似ていない程、大きな値となる。
5.相互情報量
I(X,Y)=H(X)ーH(X|Y)
=H(Y)ーH(Y|X)
=H(X)+H(Y)ーH(X,Y)
最後まで読んで頂きありがとうございます。
皆様のキャリアアップを応援しています!!

コメント