- 行列の「固有値」、「特異値」について学びたいけど理解できるか不安・・・
- 「固有値分解」、「特異値分解」を行うメリットが分からない?
- 「固有値分解」、「特異値分解」の求め方を分かりやすく教えて!
行列の「固有値」、「特異値」は「人工知能(AI:Artificial intelligence)」において利用されていますがなんとなく難しそうで、AIを学ぶ際の障壁になるケースは非常に多いです。
私は2年程前に「一般社団法人 日本ディープラーニング協会」が主催の「G検定試験」に合格しました。現在、「E資格」にチャレンジ中ですが3回不合格になり、この経験から学習の要点について学ぶ機会がありました。
そこでこの記事では、行列の「固有値」、「特異値」の求め方や、「固有値分解」、「特異値分解」を行うメリットについてポイントを解説します。
この記事を参考に「行列」を理解すれば、E資格に合格できるはずです。
目次
固有値と固有ベクトル

固有値・固有ベクトル 具体例
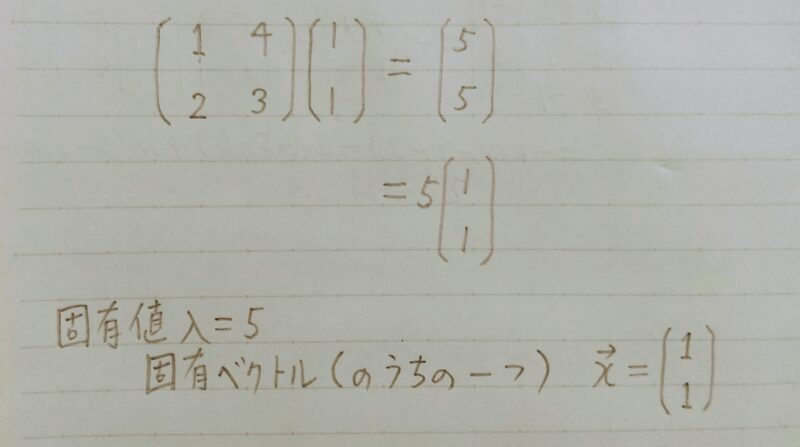
固有値・固有ベクトル 求め方
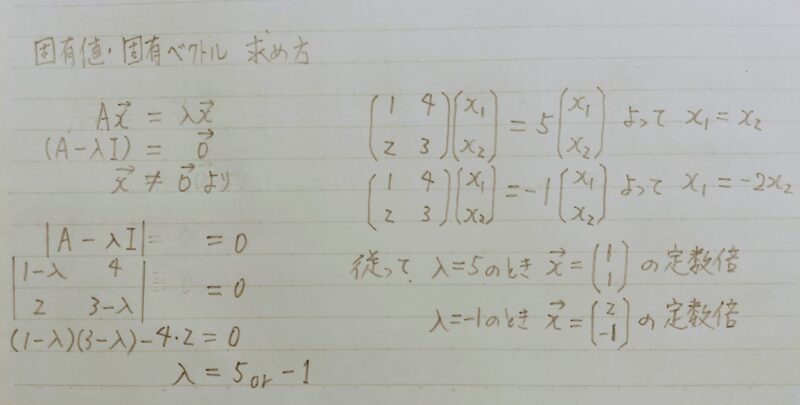
固有値・固有ベクトルを求める問題

固有値分解

固有値分解を行うメリットは行列の累乗の計算が容易になることである。
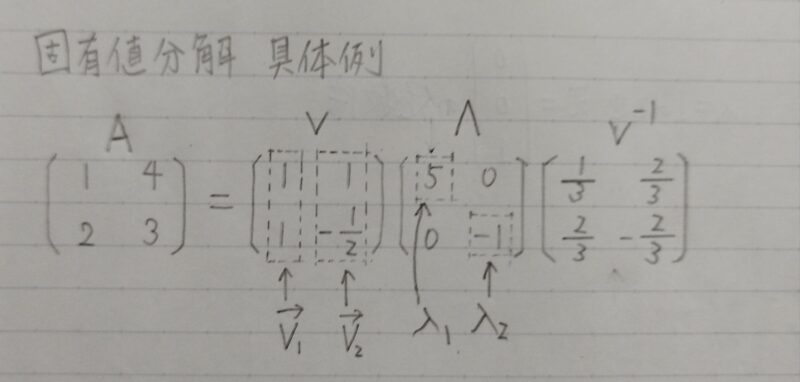
固有値分解 具体例
固有値分解を行う問題
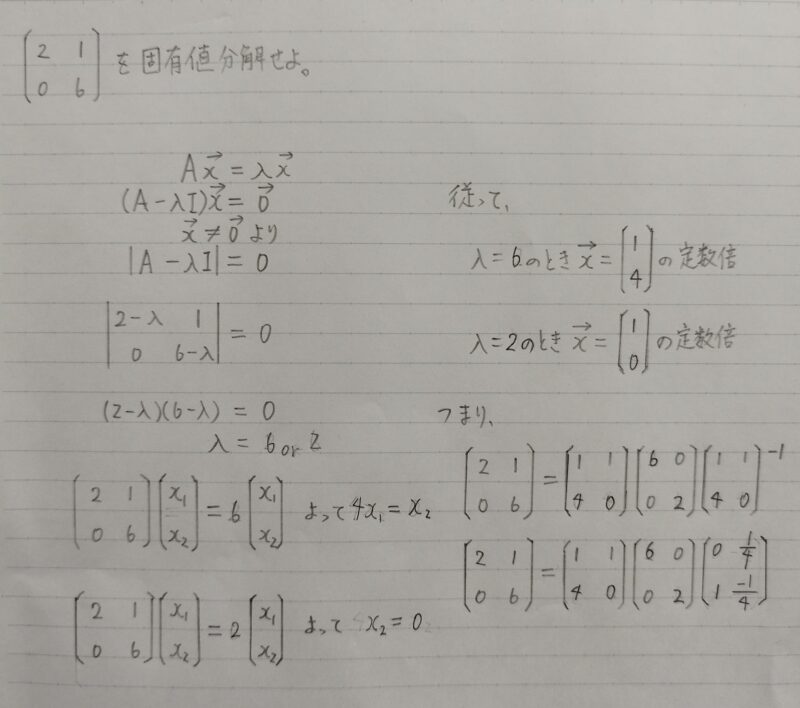
特異値分解

学生
正方行列以外は固有値分解できないの?

著者
「似た」ことは出来るよ!!
下式のような特殊な単位ベクトル(v、u)があるならば特異値分解できる。
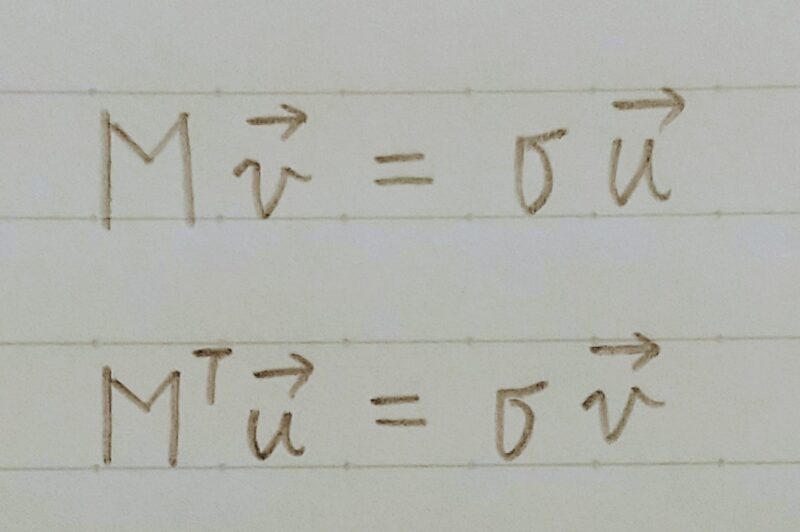

特異値分解の定義式は次のとおりだよ!!
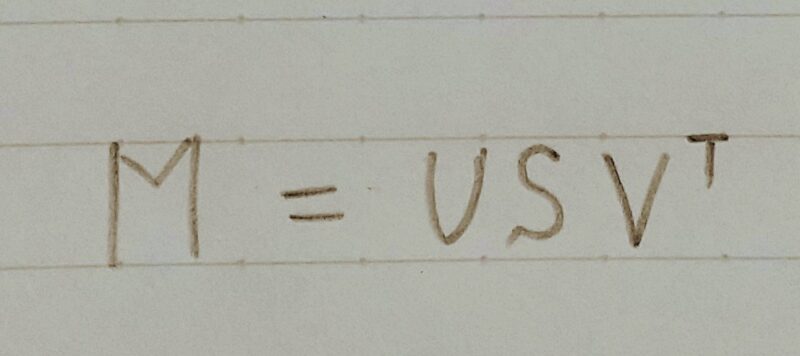

注1)UやVは直行行列(複素数を要素に持つ場合はユニタリ行列)
注2)VTのTは転置行列のこと
特異値の求め方
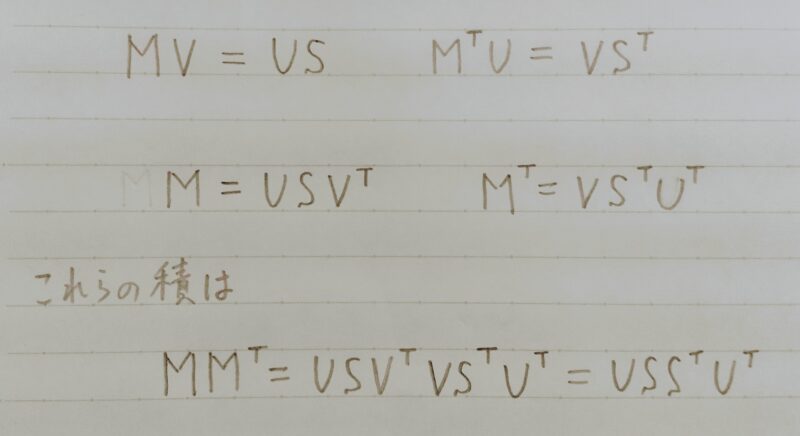
MMT を固有値分解すれば、その左特異ベクトルと特異値の2乗が求められることが分かる。
注)左特異ベクトルは単位ベクトルから作らなければならない
特異値の求め方 具体例
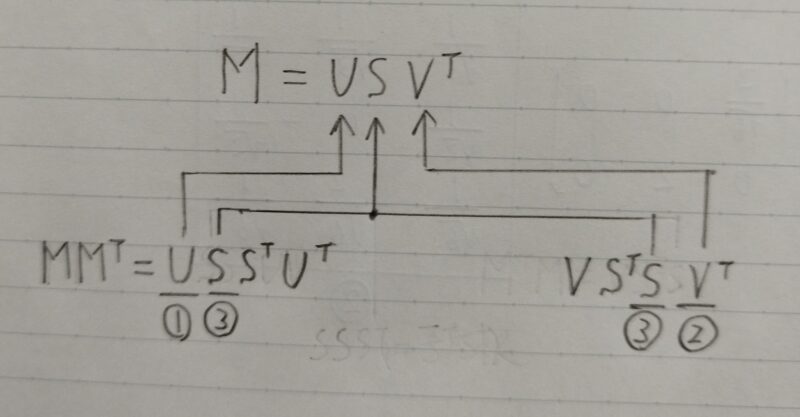


学生
MMTの特異値はどう求めるの?

著者
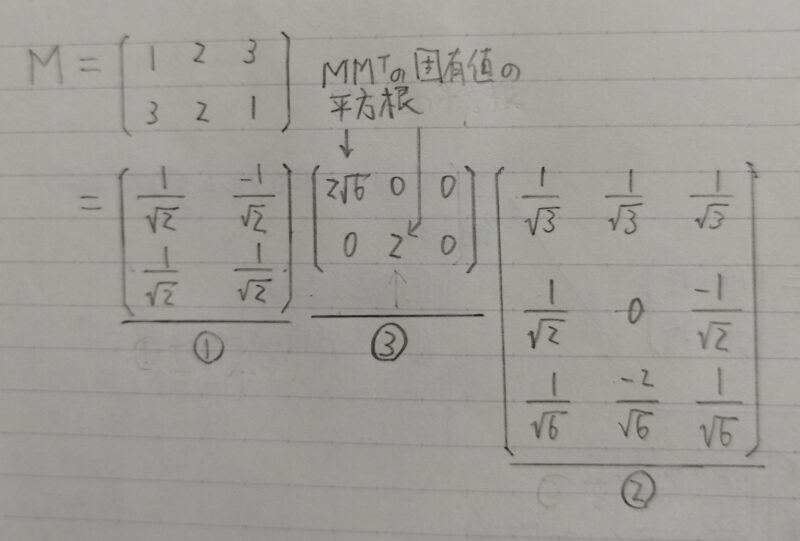
MMTの固有値λの平方根をとるんだよ?
λ=24,4→特異値は2√6,2

学生
特異値分解は面倒くさいなあ!
もっと簡単に解く方法はないの?

著者
次の性質を使うと簡単に解くことができるよ!!
- ①右特異ベクトルvの求め方
MTMの固有値はλ=24,4,0と分かっているので
MTMv=λv
MMTu=λu(MMTMv=λMv) - ②左特異ベクトルuの求め方
左特異ベクトルuは右特異ベクトルvを使って次のように表現できる。
uk=(1/σk)Mvk
uk:k番目の左特異ベクトル
σk:k番目の特異値
M:行列
vk:k番目の右特異ベクトル
固有値分解・特異値分解の利用例
- 固有値分解・特異値分解は画像データを圧縮したい場合に利用できる。
特異値分解の利用例として画像処理があり、画像データの行列から成分の小さい部分を取り除いていくと画像がぼやけていく=データ量を小さくできる。
まとめ
【行列のポイント】
- 固有値・固有ベクトルの求め方
固有値・固有ベクトルについて高校数学の復習を合わせて、AIにどのように使用されているかイメージすることが大切。 - 固有値分解
固有値分解によって行列の累乗の計算が容易になる。
行列の対角化→行列のn乗の計算回数が減る行列Xを対角化する。 - 特異値・特異ベクトルの求め方
- 特異値分解
最後まで読んで頂きありがとうございます。
皆様のスキルアップを応援しています!!

コメント