- 「Alpha Go」について学びたいけど理解できるか不安・・・
- 「Alpha Go」についてどこから学んでいいか分からない
- 「Alpha Go」を体系的に教えて!
「Alpha Go」はGoogle DeepMindによって開発されたコンピュータ囲碁プログラムでありますが、難しそうで何から学んだらよいか分からず、勉強のやる気を失うケースは非常に多いです。
私は 私は過去に基本情報技術者試験(旧:第二種情報処理技術者試験)に合格し、また2年程前に「一般社団法人 日本ディープラーニング協会」が主催の「G検定試験」に合格しました。現在、「E資格」にチャレンジ中ですが3回不合格になり、この経験から学習の要点について学ぶ機会がありました。
そこでこの記事では、「Alpha Go」の内容についてポイントを解説します。
この記事を参考にして「Alpha Go」のポイントが理解できれば、E資格に合格できるはずです。
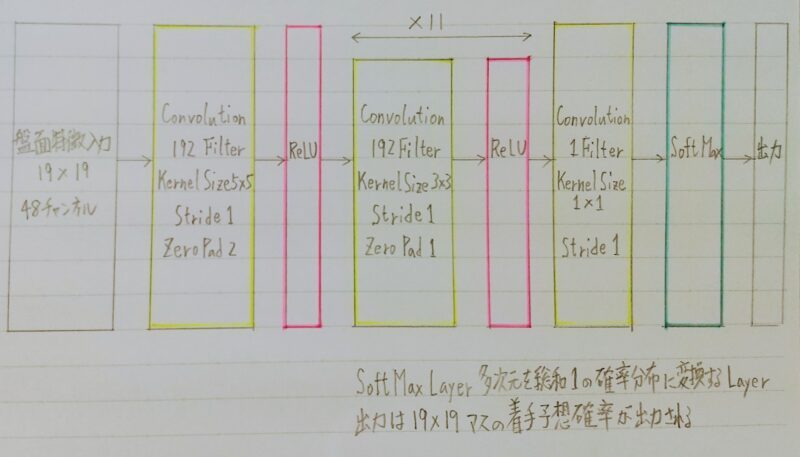
Alpha Go(Lee)のPolicyNet

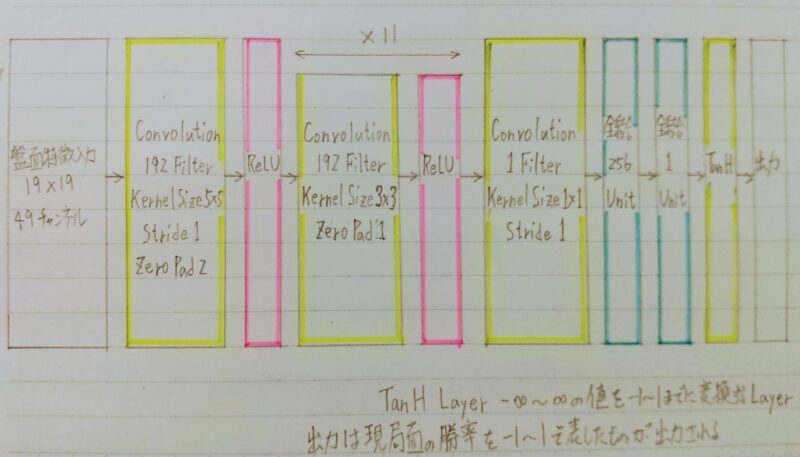
Alpha Go(Lee)のValueNet
Policy Net、Value Netの入力
| 特徴 | チャンネル数 | 説明 |
|---|---|---|
| 石 | 3 | 自石、敵石、空白の3チャンネル |
| オール1 | 1 | 全面1 |
| 着手履歴 | 8 | 8手前までに石が打たれた場所 |
| 呼吸点 | 8 | 該当の位置に石がある場合、その石を含む連の呼吸点の数 |
| 取れる石の数 | 8 | 該当の位置に石を打った場合、取れる石の数 |
| 取られる石の数 | 8 | 該当の位置に石を打たれた場合、取られる石の数 |
| 着手後の呼吸点の数 | 8 | 該当の位置に石を打った場合、その石を含む連の呼吸点の数 |
| 着手後にシチョウで 取れるか? | 1 | 該当の位置に石を打った場合、シチョウで隣接連を取れるかどうか |
| 着手後にシチョウで 取られるか? | 1 | 該当の位置に石を打たれた場合、シチョウで隣接連を取られるかどうか |
| 合法手 | 1 | 合法手であるかどうか |
| オール0 | 1 | 全面0 |
| 手番 | 1 | 現在の手番が黒番であるか?(Policy Netにはこの入力はなく、Value Netのみ) |
RollOut Policy
- ニューラルネットワークではなく線形の方策関数
- 探索中に高速に着手確率を出すために使用される
| 特徴 | 次元数 | 説明 |
|---|---|---|
| 12近傍マッチ | 1 | 一つ以上の12近傍パターン(下記)にマッチしたかどうか |
| アタリ救助 | 1 | アタリを逃げる手であるかどうか |
| 隣接 | 8 | 直前の着手と隣接したマスへの着手であるか |
| ナカデ | 8192 | ナカデのパターンにマッチするか |
| 12近傍(直前) | 32207 | 直前の着手中心のダイアモンド型12近傍パターンにマッチするか |
| 3×3近傍 | 69338 | 着手しようとしているマス中心の3×3近傍パターンにマッチするか |
| アタリ | 1 | アタリをつける手か |
| 距離 | 34 | 直前の着手と着手しようとしているマスのマンハッタン距離 |
| 12近傍 | 69338 | 着手しとうしているマス中心のダイアモンド型12近傍パターンにマッチするか |
赤字の特徴はRollOut時には使用されず、TreePolicyの初期値として使用される時に使われる。
上記の特徴が19×19マス分あり、出力はそのマスの着手予想確率となる。
Alpha Go の学習
- 教師あり学習によるRollOutPolicyとPolicyNetの学習
- 強化学習によるPolicyNetの学習
- 強化学習によるValueNetの学習
引用元:https://www.nature.com/articles/nature16961
PolicyNet の教師あり学習
- KGS Go Server(ネット囲碁対局サイト)の棋譜データから3000万局面分の教師データを用意⇒ 教師と同じ着手を予測できるよう学習を行った。
- 具体的には、教師が着手した手を1とし残りを0とした19×19次元の配列を教師とし、それを分類問題として学習した。
- この学習で作成したPolicyNetは57%程の精度である。
PolicyNet の強化学習
ValueNet の学習
- PolicyNetを使用して対局シミュレーションを行い、その結果の勝敗を教師として学習した。教師データ作成の手順は次のとおり。
- SL PolicyNet(教師あり学習で作成したPolicyNet)でN手まで打つ。
- N+1手目の手をランダムに選択し、その手で進めた局面をS(N+1)とする。
- S(N+1)からRL PolicyNet(強化学習で作成したPolicyNet)で終局まで打ち、その勝敗報酬をRとする。
モンテカルロ木探索
- モンテカルロ法を使った木の探索の事。
- 決定過程に対する、ヒューリスティクス(=途中で不要な探索をやめ、ある程度の高確率で良い手を導ける)な探索アルゴリズムである。
- コンピュータ囲碁ソフトでは現在もっとも有効とされている探索法
他のボードゲームではminmax探索やその派生形のαβ探索を使うことが多い
↓
盤面の価値や勝率予想値が必要
↓
囲碁では盤面の価値や勝率予想値を出すのが困難
盤面評価値に頼らず末端評価値(=勝敗)のみを使って探索を行うことができないか?
↓
囲碁の場合、他のボードゲームと違い最大手数はマスの数でほぼ限定されるため、末端局面に到達しやすい。
- 現局面から末端局面までランダムシミュレーション(PlayOutと呼ぶ)を多数回行い、その勝敗を集計して着手の優劣を決定する。
- 該当手のシミュレーション回数が一定回数を超えたら、その着手したあとの局面をシミュレーション開始局面とするよう、探索木を成長させる。
- 1.選択

c:勝敗期待値と着手予想確率のバランスを決めるパラメータ
基本:第1項の勝敗期待値が高いものが選択
補正:第2項がバイアス項となり選択数が少ないものが選ばれやすくなる。このときの着手予想確率はAlphaGoではPolicyNetの出力が用いられた。
- 2.評価
ValueNetでの評価を行う
その局面を開始局面として方策RollOut対局シミュレーションを行う
↓
両方の評価を合議したものをその着手の評価 - 3.バックアップ
「選択」ステップでの評価を親ノードに遡って更新する。 - 4.成長
一定回数選択されたリーフノードの合法手を展開し、新たなリーフノードとする。
- 探索木の成長を行う。
- この木の成長を行うことによって、一定条件下において探索結果は最善手を返すということが理論的に証明されている。
まとめ
【AlphaGoポイント】
- モンテカルロ木探索を採用
- 手順は、選択→評価→バックアップ→成長
- 選択では勝敗期待値と着手予想確率のバランスをとる
- 着手予想確率:PolicyNet で算出
評価:ValueNetで行う
対局シミュレーション:RollOut Policyで行う
最後まで読んで頂きありがとうございます。
皆様のキャリアアップを応援しています!!

コメント