- 「音声認識」について学びたいけど理解できるか不安・・・
- 「音声認識」についてどこから学んでいいか分からない?
- 「音声認識」の基礎を体系的に教えて!
音声データを処理する能力を持つAIの研究・開発が近年多くなされており、活用事例として音声アシスタント、スマートスピーカー等がありますが、興味があっても難しそうで何から学んだらよいか分からず、勉強のやる気を失うケースは非常に多いです。
私は過去に基本情報技術者試験(旧:第二種情報処理技術者試験)に合格し、また2年程前に「一般社団法人 日本ディープラーニング協会」が主催の「G検定試験」に合格しました。現在、「E資格」にチャレンジ中ですが3回不合格になり、この経験から学習の要点について学ぶ機会がありました。
そこでこの記事では、「音声認識」の全体像やこれまでの流れが分かるよう音声認識の内容について体系的に解説します。
この記事を参考にして「音声認識」の基礎が理解できれば、E資格に合格できるはずです。
<<音声認識の概要に関する学習のポイントを今すぐ知りたい方はコチラ
音声認識の概要
- 音声認識(ASR:Automatic Speech Recognition)
- 音声データを処理する能力を持つAIの研究・開発が近年多くなされている。
・利便性の向上
・業務の生産性の向上
・他の技術と組み合わせることができる - 活用事例:
・音声アシスタント
・スマートスピーカー
・会議などで使われる自動議事録AI - 音声認識をタスクとしたデータ分析コンペも多数
Kaggle Freesound Audio Tagging 2019
ー 短い音声データからギターや犬の鳴き声などをタグ付けする。
Kaggle BirdCLEF2021:Processing audio data
ー鳥の鳴き声の音声データから、各鳴き声に対応する鳥の種類を
推測するタスク - 音声データをどうやって扱うか?
そもそも、音声データとは何だろうか
音声データとは
音はどのように耳に伝わるか?
- 物体の振動による空気の振動
- 空気のない宇宙では音は聞こえない
- 周波数:一秒あたりの振動数(周期数)
- 角周波数:周波数を回転する角度で表現
音波と機械学習
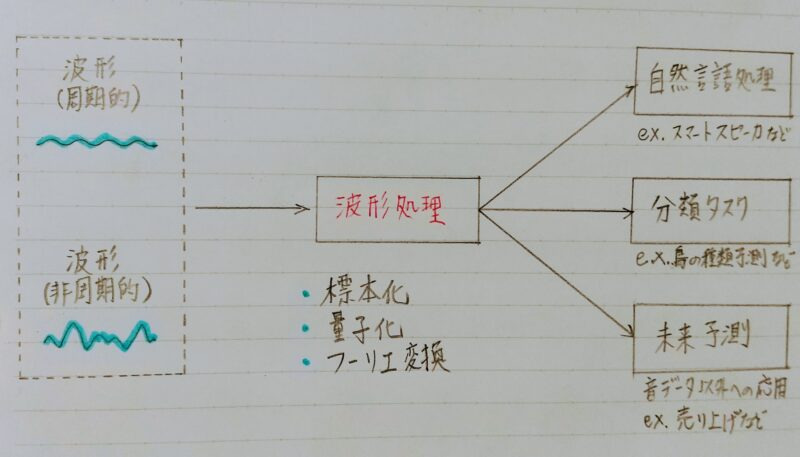
標本化・量子化とは
①標本化(サンプリング):一定の周期(サンプリング周期)でデータを抽出
引用元:「ポンパス」
②量子化:抽出したデータを数値で置き換える
③符号化:数値を『0』、『1』からなるディジタルデータに変換
標本化周波数とは
標本化周波数(サンプリング周波数)とは・・・
引用元:「IT用語辞典 eーWords」
アナログ信号をデジタルデータに変換する際に、信号の変位を測定するサンプリング(標本化)を行う頻度。1秒間に何回サンプリングを行うかをHz(ヘルツ)で表す。
フーリエ変換とは
目的:波形を機械学習の入力とするために行う(標本化、量子化と併用)
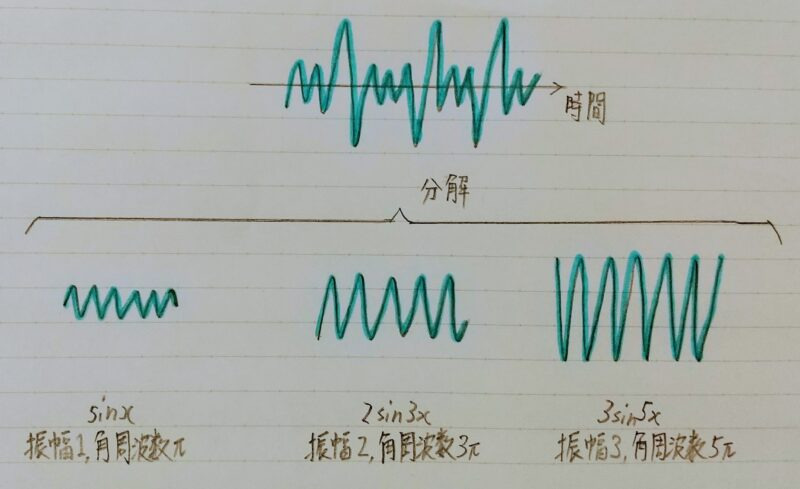
前提:あらゆる波形(周期的・非周期的)は、正弦波・余弦波を用いて表現できる
振幅の周波数が分かれば、波の特性が分かる!
振幅h、角周波数の正弦波:hsinω
振幅h、角周波数の余弦波:hcosω
定義:ある波形f(t)から振幅・角周波数を表す
関数F(ω)に変換する作業
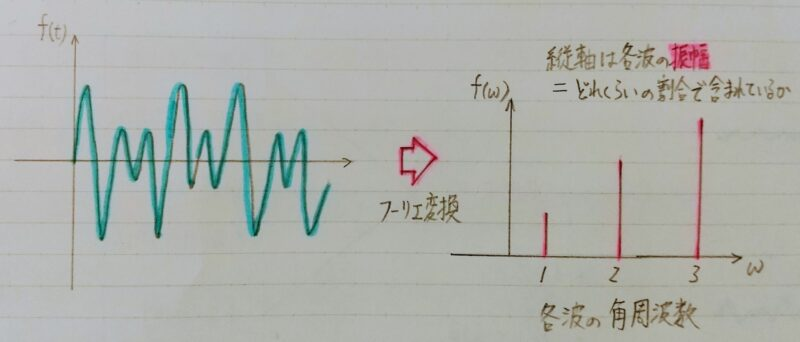
↑上の図をスペクトルと呼ぶ
フーリエ変換の概算(補足)
■全ての波形は正弦波・余弦波で表せる。
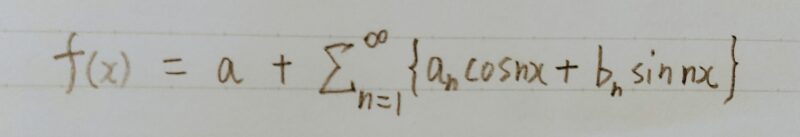
(マクローリン展開より)
■オイラーの公式:
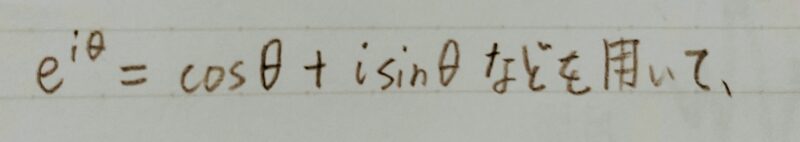

スペクトル
周期的波形 非周期的波形
↓ ↓
離散ベクトル 連続スペクトル
- 目的:現実的である非周期音声データの分析
- 窓関数:波形を特定の時間区間(窓)で区切る
- 窓の大きさが問題となる
窓の関数の大きさにより元の波形と異なる結果となる - 普通の窓:矩形窓
- ハミング窓
窓のつなぎ目を滑らかにするために区間ごとの波形関数にかける関数
- DFT:離散フーリエ変換
窓1つ=8サンプル → サンプルの個数分の振幅と周波数のペア - FFT:高速フーリエ変換
窓のサンプルのうち、偶数番目と奇数番目を別々に測定
窓に含まれるサンプルN個(Nは2のべき乗:8,16,32,・・・,1024,2048,・・・)
→ N/2個のサンプルを測定→高速化
Q.サンプリング周波数16kHzの信号に1024サンプルの窓をかけてフーリエ変換した場合を考える。このときに得られる周波数スペクトルは?
A.0Hzから16kHzまでの、513個の等分点における周波数情報が得られる。
その他の技術
- 人間の聴覚特性に基づいた尺度
- 周波数の低い音に対して敏感で、周波数の高い音に対して鈍感であるという性質がある
⇒ 低周波域では分解能が高く、高周波域では分解能が低い
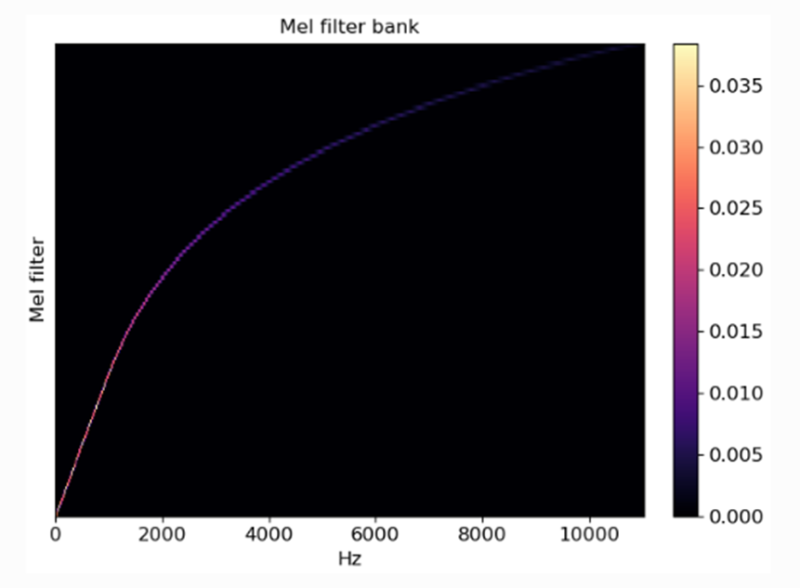
上図引用元:https://librosa.org/doc/main/generated/librosa.filters.mel.html
- 逆フーリエ変換
・振幅・周波数から元の波形を構築する作業 - ケプトプラス
・フーリエ変換したものの絶対値の対数
を逆フーリエ変換して得られるもの
・音声認識の特徴量として利用される。
まとめ
最後まで読んで頂きありがとうございます。
皆様のキャリアアップを応援しています!!

コメント