- 「深層学習(Deep Learning)」について学びたいけど理解できるか不安・・・
- 「深層学習(Deep Learning)」についてどこから学んでいいか分からない?
- 「深層学習(Deep Learning)」の全体像を分かりやすく教えて!
「深層学習(Deep Learning)」は既に様々な商品・サービスに組み込まれて利活用が始まっている注目の技術ですが、興味があっても難しそうで何から学んだらよいか分からず、勉強のやる気を失うケースは非常に多いです。
私は過去に基本情報技術者試験(旧:第二種情報処理技術者試験)に合格し、また2年程前に「一般社団法人 日本ディープラーニング協会」が主催の「G検定試験」に合格しました。しかし「E資格」を受験し3回不合格になった苦い経験があります。この経験より不合格になった原因を追究し学習すべき要点を整理しました。
そこでこの記事では、「深層学習(Deep Learning)」の概要について解説します。
この記事を参考にして「深層学習」の概要を理解できれば、E資格に合格できるはずです。
プロローグ
- 識別と生成
機械学習(深層学習)モデルを入力・出力の目的で分類したもの
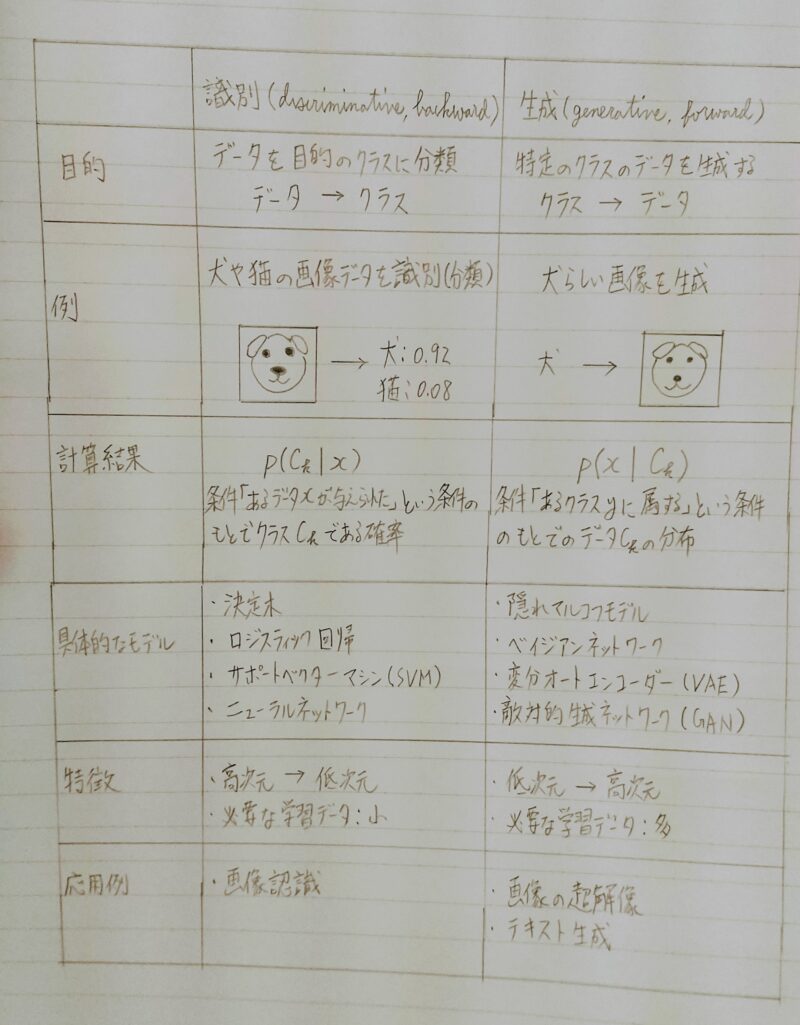
P(Ck|x)・・・入力データxに対するクラスCkの条件付き確率(事後確率)
引用元:【機械学習】統計学(条件付き確率とベイズ則)とは?
ベイズの定理とは・・・
ベイズの定理 P(A):事象Aが起きる確率
P(B):事象Bが起きる確率
P(B|A):ある事象Aが与えられた下で、Bとなる確率
P(A|B):ある事象Bが与えられた下で、Aとなる確率
引用元:【機械学習】統計学(条件付き確率とベイズ則)とは?
識別モデルと識別関数
- 特徴
・確率に基づいた識別境界を設定
⇒ 最大値<識別境界の場合は回答しないモデルとすることが可能
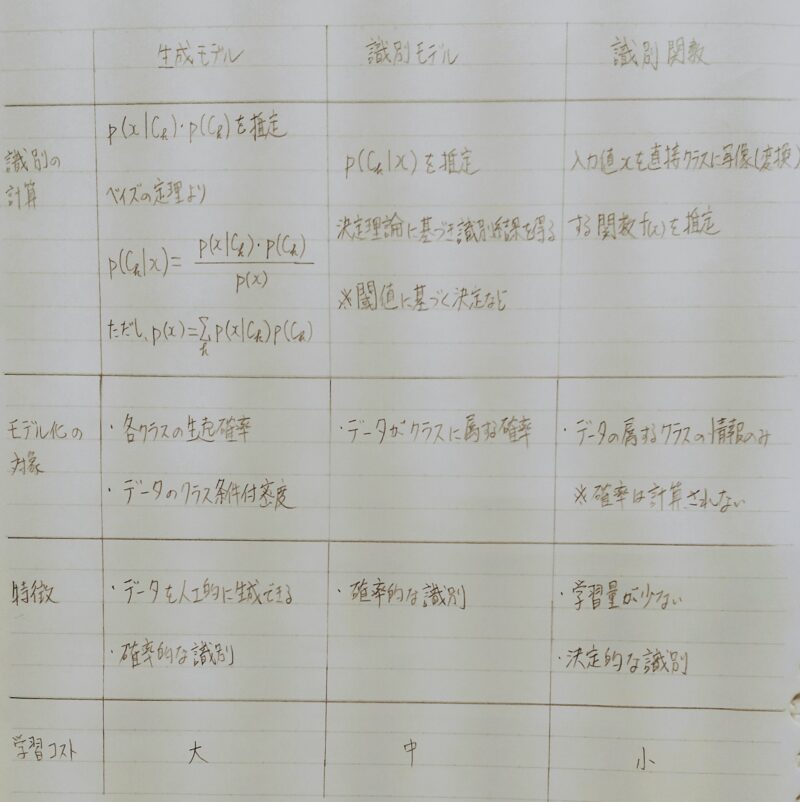
・高次元→低次元、学習データ少ない - 識別の計算:P(Ck|x)を推定 ※閾値に基ずく決定など ← 条件付き確率
- モデル化の対象:データがクラスに属する確率
- 特徴:確率的な識別
- 学習コスト:中
- 具体例:ニューラルネットワーク
- 識別の計算:
入力値xを直接クラスに写像(変換)する関数(x)を推定 - モデル化の対象:
・データに属するクラスの情報のみ
・確率は計算されない - 特徴:
・学習量が少ない
・決定的な識別 - 学習コスト:小
- 具体例:
決定木、ロジスティック回帰、サポートベクターマシン(SVM)
「生成モデル」の開発アプローチ
- 例題:生成モデルではあるデータxについて、各Ciにおけるxとなる確率すなわちP(x|Ci)と、Ciが出現する確率P(Ci)を求めることでxがあるCiに分類される確率を求める。ある学生の性別データから学校Aか学校Bかを判別するモデルを考える。
学校Aの男女比は7:3で生徒数は1000人,学校Bの男女比は2:8で生徒数は250人であるとする。ある入力データxiについて性別が女子であった時、学校Aに属する確率を求めよ。ただし、ここで性別は男子もしくは女子しか考えないものとする。
- 回答:
| 学校A (C1) | 学校B (C2) | 計 | |
|---|---|---|---|
| 男子 | 700 | 50 | 750 |
| 女子(x) | 300 | 200 | 500 |
| 計 | 1,000 | 250 | 1,250 |

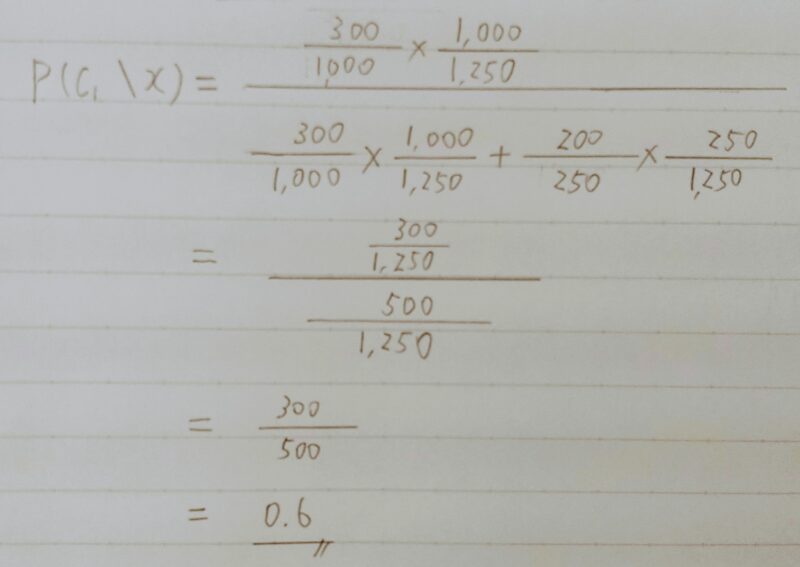
- 例題:識別モデルでは直接、事後確率p(Ck|x)を決める推論問題を解く。複数の球が入った箱があり、球の色が白か赤、大きさは大きいものと小さいものがある。球の数の分布が次のような表の様になっていることが分かっている。
このときp(Ck=白|x=大)を求めよ。ただし、Ckは白か赤の二値、xは”大”と”小”の二値しかとらないものとする。
| 大 | 小 | 計 | |
|---|---|---|---|
| 白 | 12個 | 28個 | 40個 |
| 赤 | 18個 | 4個 | 22個 |
| 計 | 30個 | 32個 | 62個 |
- 回答:

識別器における生成モデルと識別モデル
- データの分布は分類結果より複雑なことがある。
- データの分布を推定
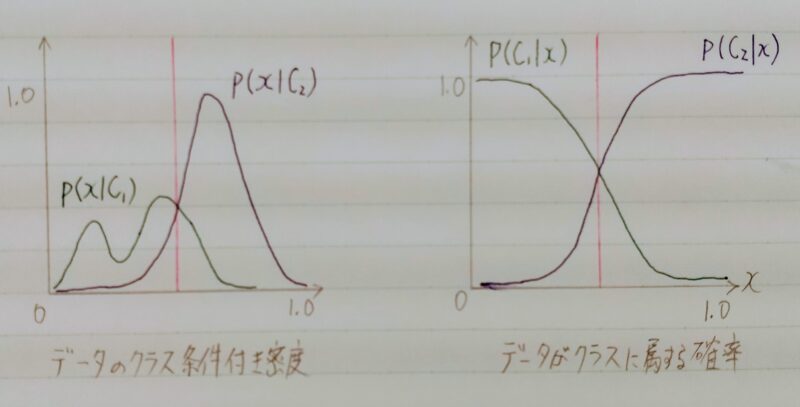
| データのクラス条件付き密度 (上図左) | データがクラスに属する確率 (上図右) |
|---|---|
| ・分類結果より複雑 ・生成モデルはこの分布を推定 ・計算量が多い | 分類結果を得る 分類モデルのアプローチ |
識別器における識別モデルと識別関数
識別モデル:識別結果の確率が得られる。
識別関数:識別結果のみ。

| 識別モデル (確率的識別モデル) | 識別関数 (決定的識別モデル) | |
|---|---|---|
| 仕組み | 推論:入力データを基に事後確率を求める。 決定:事後確率p(Ck|x)を基に識別結果を得る。 | 入力データから識別結果を一気に得る。 |
| 特 徴 | 間違いの程度を測ることが出来る。推論結果の取り扱いを決められる(棄却など)。 ⇒確率に基づいた識別境界を設定し、最大値が識別境界を下回った場合は回答しないモデルとすることができる。 | 間違いの程度を測ることができない。 |
| 具体例 (犬と猫の2値分類の場合) | 出力値は「犬:0.93、猫:0.07」や「犬:0.55、猫:0.41」のようにその予測の確率も把握が可能 ∴「1つのカテゴリが0.7以上の場合に回答する」のように、識別境界を設定が可能 | 直接クラスの番号を出力すると、出力値は「犬」または「猫」となる。 |
万能近似定理と深さ
あらゆる問題で性能の良い汎用的な最適化戦略は理論上不可能であり、ある戦略が他の戦略より性能がよいのは、現に解こうとしている特定の問題に対して特殊化(専門化)されている場合のみである。
この定理は、問題領域に関する知識を使わずに遺伝的アルゴリズムや焼きなまし法などの汎用探索アルゴリズムを使うことに反対する論拠として使われる。
引用元:Wikipedia
↓
「ニューラルネットワーク」はどんな関数でも近似できる(=万能近似定理)
ニューラルネットワークの全体像
| 区分 | できること | 具体例 |
| 回帰 | 結果予想 | 売上予想 |
| 株価予想 | ||
| ランキング | 競馬予想順位 | |
| 人気予想順位 | ||
| 分類 | 分類 | 猫写真の判別 |
| 手書き文字認識 | ||
| 花の種類分類 |
- 連続する実数値を取る関数の近似
- 回帰分析
・線形回帰
・回帰木
・ランダムフォレスト
・ニューラルネットワーク(NN) ← 万能近似定理
- 性別(男あるいは女)や動物の種類など離散的な結果を予想するための分析
- 【分類分析】
・ベイズ分類
・ロジスティック回帰
・決定木
・ランダムフォレスト
・ニューラルネットワーク(NN) ← 万能近似定理
- 深層学習:中間層が4つ以上
・自動売買(トレード) 全銘柄の平均株価→ある1社の株価を予測
・チャットボット 質問の文章→回答の文章
・翻訳 翻訳したい文章→翻訳した文章
・音声解釈 空気の振動数→文字の出力
・囲碁(AlphaGo)、将棋AI
確認テスト
- Q1.ディープラーニングは何をしようとしているのか?
- A1.明示的なプログラムの代わりに多数の中間層を持つニューラルネットワークを用いて、入力値から目的とする出力値に変換する数学モデルを構築すること。
- Q2.何を最適化するのか?
- A2.③重み(W)、④バイアス(b)
Q3.次のネットワークを紙に書け。
入力層:2ノード1層
中間層:3ノード2層
出力層:1ノード1層
A3.
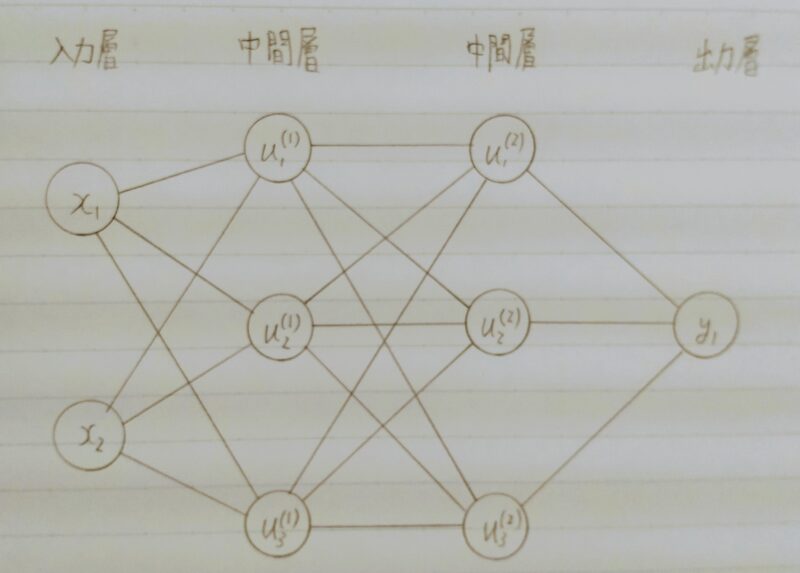
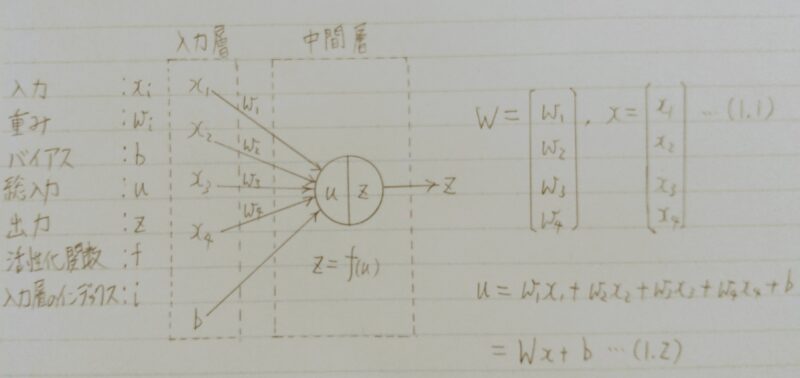
入力層~中間層
確認テスト
- Q.上図式に動物分類の実例を入れてみよう。
- A.動物種類分類ネットワーク
x1=10 体長
x2=30 体重
x3=300 ひげの本数
x4=15 毛の平均長
X5=50 耳の大きさ
x6=1.8 眉間/目 鼻 距離比
x7=20 足の長さ
- Q.下記の数式をPythonで書け。
u=w1x1+w2x2+w3x3+w4x4+b
=Wx+b・・・(1.2) - A.# 1層の総入力
u1=np.dot(x, W1) + b1
Q.1-1のファイルから中間層の出力を定義しているソースを抜き出せ。
A.# 2層の総入力
u2 = np.dot(z1, W2) + b2
# 2層の総出力
z2 = functions.relu(u2)
活性化関数
- ニューラルネットワークにおいて、次の層への出力の大きさを決める非線形の関数。
- 入力値の値によって、次の層への信号のON/OFFや強弱を定める働きをもつ。
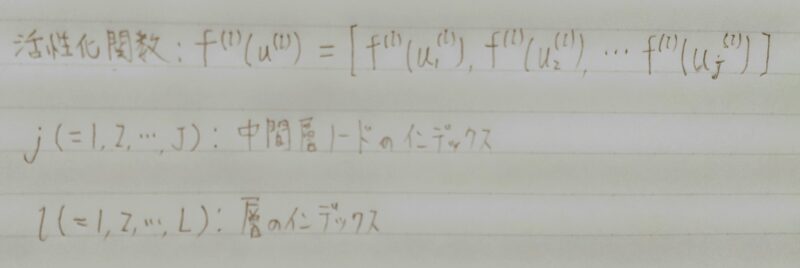
中間層の活性化関数
- 閾(しきい)値を超えたら発火する関数であり、出力は常に1か0。
- パーセプロトン(ニューラルネットワークの前身)で利用された関数。
- 【課題】0~1間の間を表現できず、線形分離可能なものしか学習できなかった。

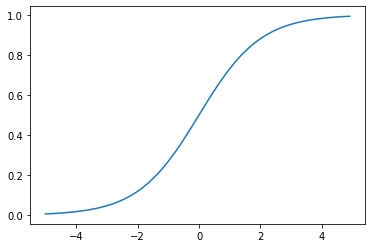
- 0~1の間を緩やかに変化する関数
ステップ関数ではON/OFFしかない状態に対し、信号の強弱で伝えられるようになる - 予想ニューラルネットワーク普及のきっかけとなった。
- シグモイド関数の微分 ⇒ f(x)’ = (1ーf(x))・f(x)
- 【課題】大きな値では出力の変化が微小なため勾配消失問題を引き起こすことがあった。
- 今最も使われている活性化関数
- シグモイド関数の勾配消失問題を解消
- 勾配消失問題の回避とスパース化に貢献することで良い成果をもたらしている。
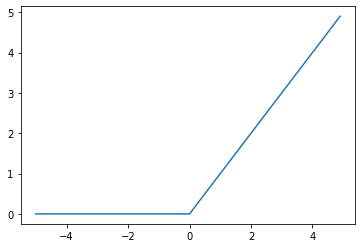
- log(1+exp(x))
- ReLU関数に似ている。xが小さい時にはy=0、xが大きい時にはy=x
- 全区間で微分可能
(ReLU関数はx=0で非連続で微分不可)
確認テスト
Q1.線形と非線形の違いを図に書いて簡易に説明せよ。
A1.
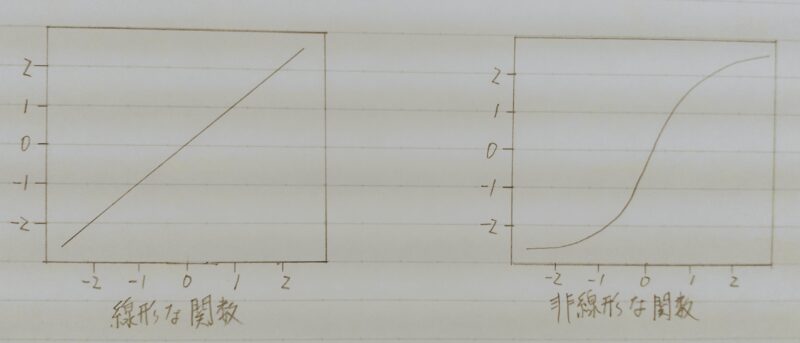
| 線形な関数 | 非線形な関数 |
|---|---|
| 入力と出力の関係が比例 ・加法性:f(x+y)=f(x)+f(y) ・斉次性:f(kx)=kf(x) を満たす | 入力と出力の関係が比例ではない。 ・加法性・斉次性を満たさない |
出力層
- 誤差関数
- 出力層の活性化関数
各クラスの確率を出す
誤差関数
- 誤差関数が二乗誤差の場合


- ①誤差関数はなぜ、引き算ではなく二乗するの?
- ②上式の1/2はどういう意味を持つの?

- ①引き算を行うだけでは、正負両方の値が発生してしまうからだよ!!
- ②誤差関数の微分を簡単にするためだよ!!(本質的な意味はないよ。)

誤差関数はなぜ、四乗ではいけないの?
四乗なら二乗と同じように正負両方の値が発生しないよ!

四乗と二乗は同じような特徴になるから、わざわざ面倒な四乗の計算をする必要はないんだよ!!
loss = functions.mean_squared_error(d, y)
※本来ならば分類問題の場合
誤差関数にクロスエントロピー誤差を用いるのでコードは
loss = cross_entropy_error(d, y)
となる。
出力層の活性化関数
出力層の中間層との違い
| 出力層 | 中間層 | |
|---|---|---|
| 値の強弱 | 信号の大きさ(比率)はそのままに変換 | 閾(しきい)値の前後で信号の強弱を調整 |
| 確率出力 | 分類問題の場合、出力層の出力は0~1の範囲に限定し、総和を1とする必要がある。 | 分類問題の場合、出力層の出力は0~1の範囲に限定する必要はない。 |
出力層用の活性化関数

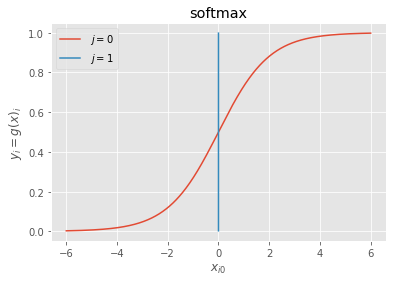
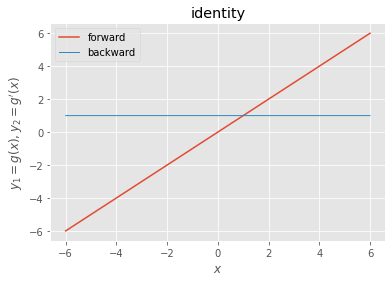
- シグモイド(ロジスティック)関数
上図の組合せを間違えなければある程度の精度が得られるニューラルネットワークを作ることができるよ!!
※バイナリクロスエントロピー損失:データのクラスが2クラスの場合に使用。
2クラスというのはデータの種類が2つであることを意味する。
バイナリクロスエントロピー損失は一種の距離を表すような指標で、ニューラルネットワークの出力と正解との間にどの程度の差があるのかを示す尺度。
・数式とコード
シグモイド関数 f(u) = 1/(1+e-u)
def sigmoid(x): return 1/(1 + np.exp(x))

・数式とコード
誤差関数
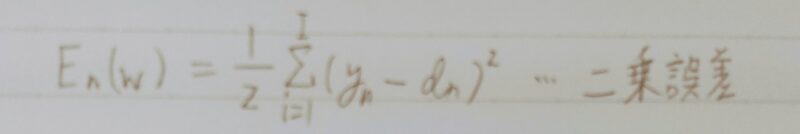
def mean_squared_error(d, y):
return np.mean(np.square(d – y)) / 2 ←平均二乗誤差
確認テスト
- Q1.・下式はなぜ、引き算ではなく2乗するか述べよ。
・下式の1/2はどういう意味を持つか述べよ。

- A1.
・2乗する理由
引き算を行うだけでは、各ラベルでの誤差で正負両方の値が発生し、全体の誤差を正しくあらわすのに都合が悪い。2乗してそれぞれのラベルでの誤差を正の値になるようにする。
・1/2する理由
実際にネットワークを学習する時に行う誤差逆伝播の計算で、誤差関数の微分を用いるが、その際の計算式を簡単にするため。本質的な意味はない。
- Q2.①~③の数式に該当するソースコードを示し、一行づつ処理の説明をせよ。
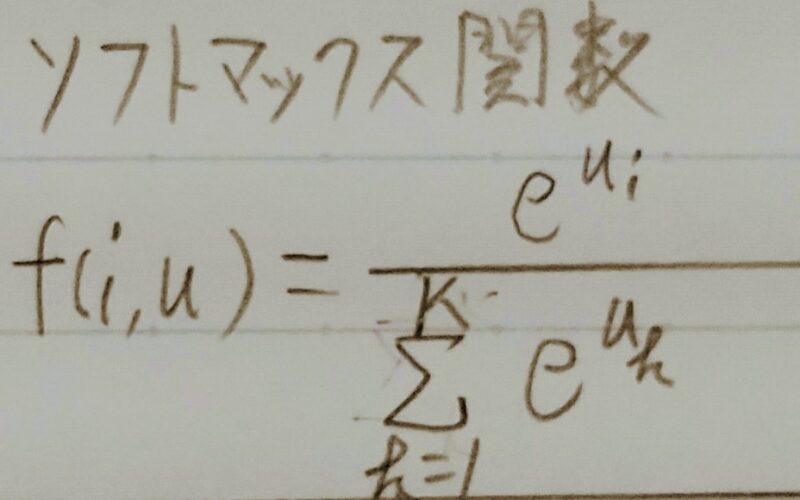
- A2.def softmax(x):
if x.ndim == 2:
x = x.T
x = x – np.max(x, axis=0)
y = np.exp(x) / np.sum(np.exp(x), axis=0)
return y.T
x = x – np.max(x) #オーバーフロー対策
return np.exp(x) / np.sum(np.exp(x))
- Q3.
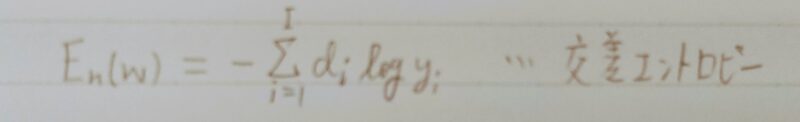
①~②の数式に該当するソースコードを示し、一行ずつ処理を説明せよ。
- A3.
def cross_entropy_error(d, y):
if y.ndim == 1:
d = d.reshape(1, d.size)
y = y.reshape(1, y.size)
# 教師データがone-hot-vectorの場合、正解ラベルのインデックスに変換
if d.size == y.size:
d = d.argmax(axis=1)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), d] + 1e-7)) /batch_size
勾配降下法
学習を通して誤差を最小にするネットワークを作成すること
→ 誤差E(w)を最小化するパラメータwを発見すること
⇒ 勾配降下法を利用してパラメータを最適化
- 勾配降下法
- 確率的勾配降下法
- ミニバッチ勾配降下法
勾配降下法(Gradient Descent)
E(誤差関数)の値をより小さくする方向にw(重み)及びb(バイアス)を更新し次の周(エポック)に反映
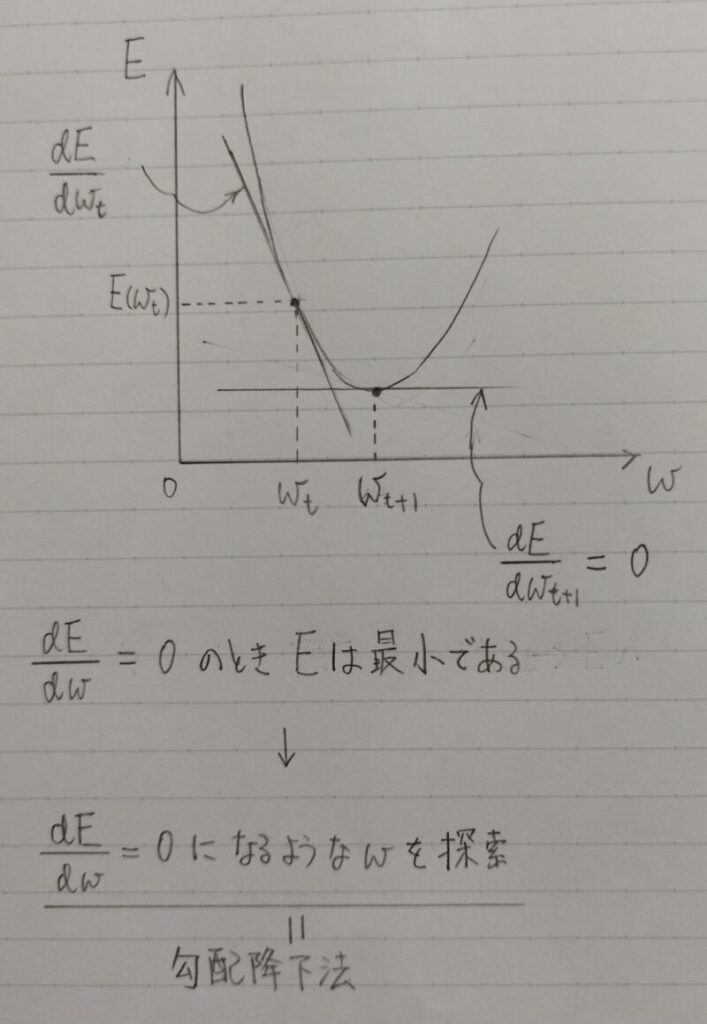
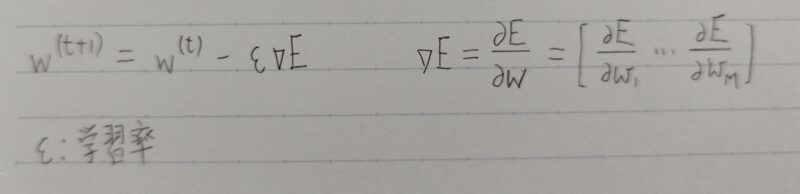
- 大きすぎた場合:最小値にいつまでも辿り着かず発散
- 小さすぎた場合:収束するまでに時間がかかる
- 勾配降下法の工夫(例)
学習率を最初は大きくし、学習が進むにつれて小さくする。
勾配降下法の「学習率」の決定、収束性向上のためのアルゴリズムの代表例は下記のとおり。
詳細は「【深層学習】性能向上の方法とは?」を参照
確率的勾配降下法(SGD:Stochastic Gradient Descent)

| メリット | デメリット | |
|---|---|---|
| 確率的勾配降下法 | ・データが冗長な場合の計算コストの軽減 ・望まない局所極小解に収束するリスクの軽減 ・オンライン学習ができる。 ・パラメータの更新量は初期値に依存しない。 | ・結果は学習率に依存する。 ・訓練データの順番を変えると 結果も変わる可能性がある。 |
「オンライン学習」とはどういう意味?
- オンライン学習とは学習データが入ってくる度に都度パラメータを更新し、学習を進めていく方法のことだよ!!
- バッチ学習とは一度に全ての学習データを使ってパラメータ更新を行う方法だよ!!
ちなみにバッチ(batch)とは「束」とか「群」という意味だよ。
【勾配降下法と比べた時の確率的勾配降下法の特徴】
| ホールドアウト法 | 確率的勾配降下法 | |
|---|---|---|
| 計算コスト (1度のパラメータ更新) | 大きい | 小さい |
| 計算コスト (大規模データ) | 大きい | 小さい |
| 精度 (1度のパラメータ更新) | 高い | 低い |
| 学習中における新しいデータの利用 | 不可 | 可 |
【例題】
Q1.以下の訓練データが与えられたとする。
| x | y | |
|---|---|---|
| ① | -1.0 | 1.0 |
| ② | 0.0 | 0.6 |
| ③ | 3.0 | ー0.8 |
y=ax+bと仮定し、そのパラメータa,bを求める。このとき訓練データとy=ax+bの誤差を最小化する目的関数E(a,b)は下式とする。
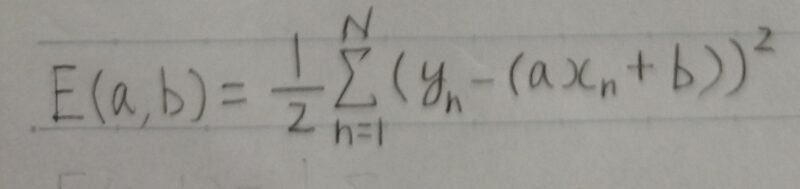
目的関数のa,bに関する偏微分∂E/∂a、∂E/∂bはどのように表せるか?
A1.
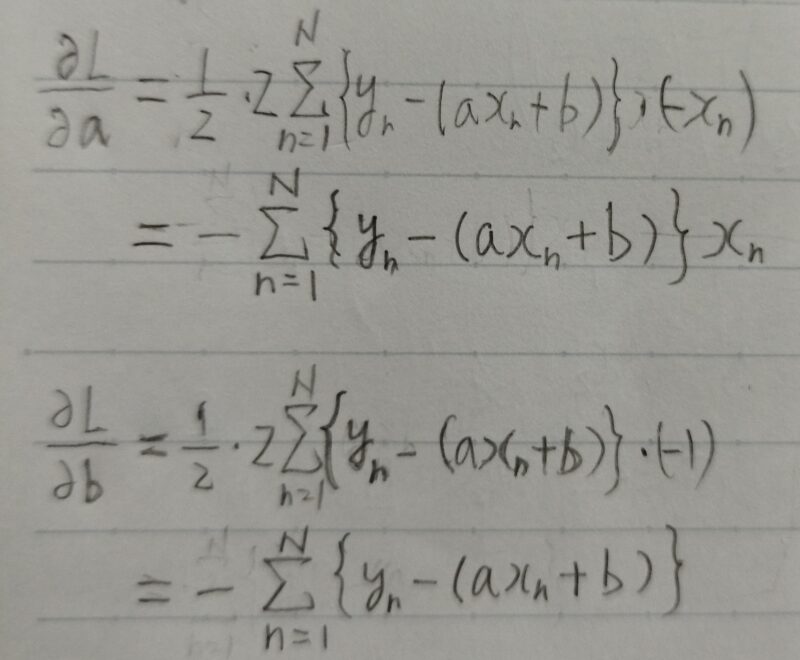
Q2.確率的勾配降下法で目的関数E(a,b)を最小化すると1回目のパラメータa,bの更新量は各々いくらになるか。ただしa,bの初期値をそれぞれ1.0,0.0、学習率μ=0.1,1回目の訓練サンプルをx=-1.0とする。
A2.確率的勾配降下法(SDG)は下式①②で表現できる。
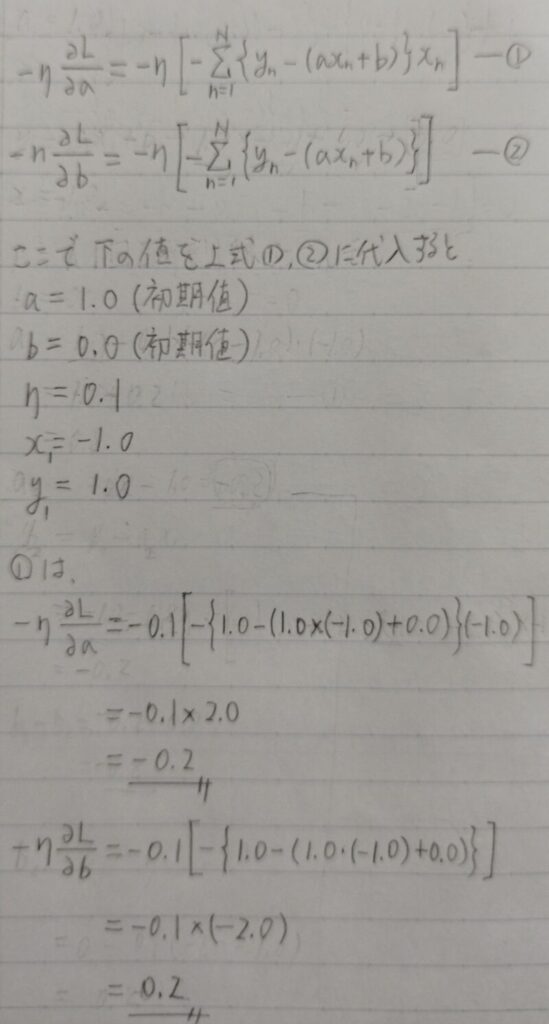
ミニバッチ勾配降下法
- 現在、ディープニューラルネットワークで使用される一般的な手法

- 確率的勾配降下法のメリットを損なわず、計算機の計算資源を有効利用できる→ CPUを利用したスレッド並列化やGPUを利用したSIMD並列化
- 補足1)スレッド並列化:複数の演算器を起き、各演算器は一つのスレッドを実行する。つまり各スレッドが一つの仕事を担当し、複数のスレッドを並列に実行する方法。現在の多くのGPUが採用しているSIMT方式は、スレッド並列の実行を行う。
- 補足2)SIMD(Single Instruction Multiple Data):コンピュータやマイクロプロセッサで並列処理を行なうための設計様式の一つで、一つの命令を同時に複数のデータに適用し、並列に処理する方式。そのような処理方式をベクトル演算、ベクトル処理などと呼ぶことがある。
Pythonコード
ミニバッチ学習で用いられるPythonコード
(編集中)
確認テスト
- Q1.該当するソースコードを探してみよう。
- A1. w(t+1) = w(t) – εΔE
ΔE = δE/δw=[δE/δw1・・・δE/δwM]
- Q2.オンライン学習とは何か2行でまとめよ。
- A2.オンライン学習とは学習データが入ってくる度に都度パラメータを更新し、学習を進めていく方法。
一方、バッチ学習では一度に全ての学習データを使ってパラメータ更新を行う。
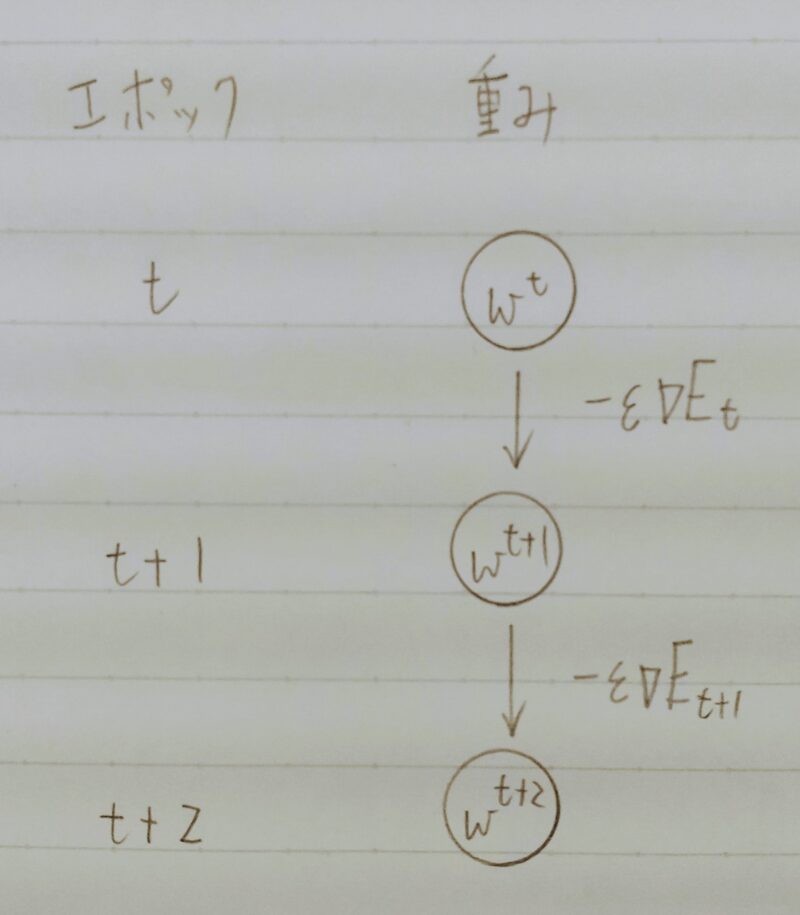
- Q3. w(t+1) = w(t) – εΔEt
上式の意味を図に書いて説明せよ。 - A3.
誤差逆伝播法
誤差勾配の計算
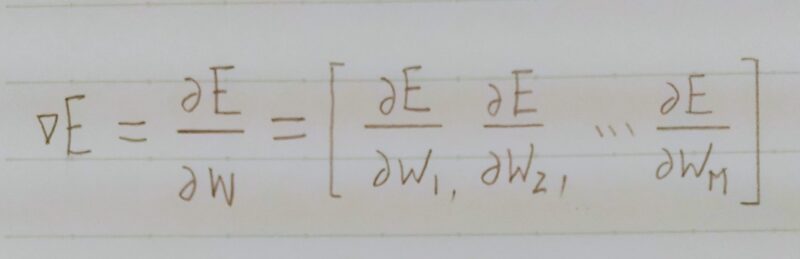

上式の誤差勾配はどう計算するの?

下のように数値微分するよ
- プログラムで微小な数値を生成し疑似的に微分を計算する一般的な手法
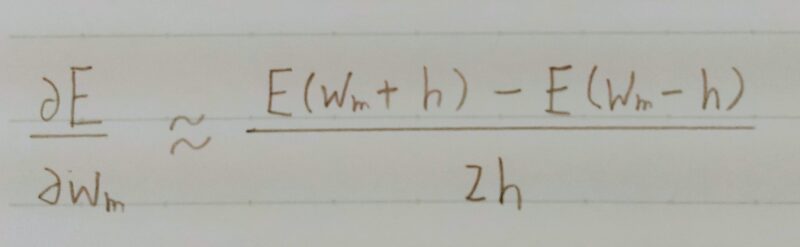
↑
m番目のwを微小変化させた状態で誤差Eを全てのwについて計算
- 数値微分のデメリット
各パラメータwmそれぞれについてE(wm +h)やE(wm – h)を計算するために、順伝播の計算を繰り返し行う必要があり負荷が大きい
↓
誤差逆伝播法を利用
- 算出された誤差を、出力層側から順に微分し、前の層前の層へと伝播。 最小限の計算で各パラメータでの微分値を解析的に計算する手法

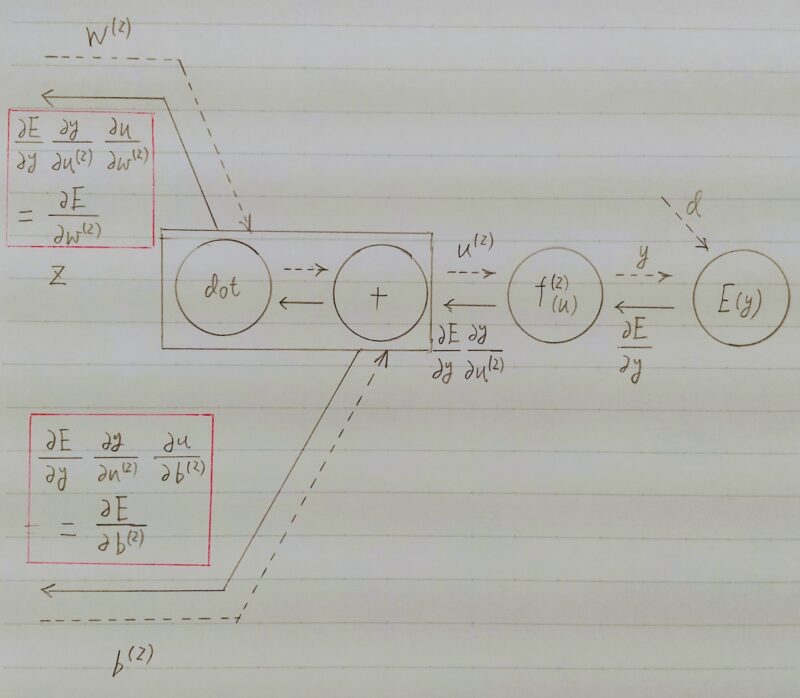
上図より、誤差逆伝播法を用いて計算結果(=誤差)から微分を逆算することで、不要な再帰的計算を避けて微分算出できる。
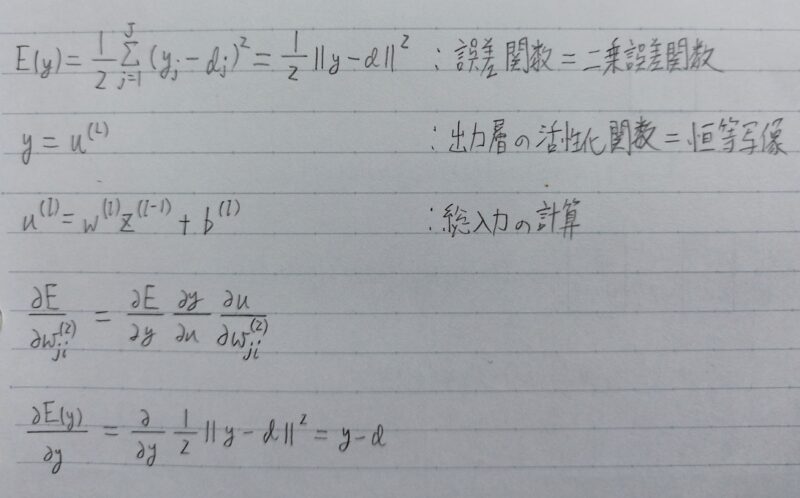
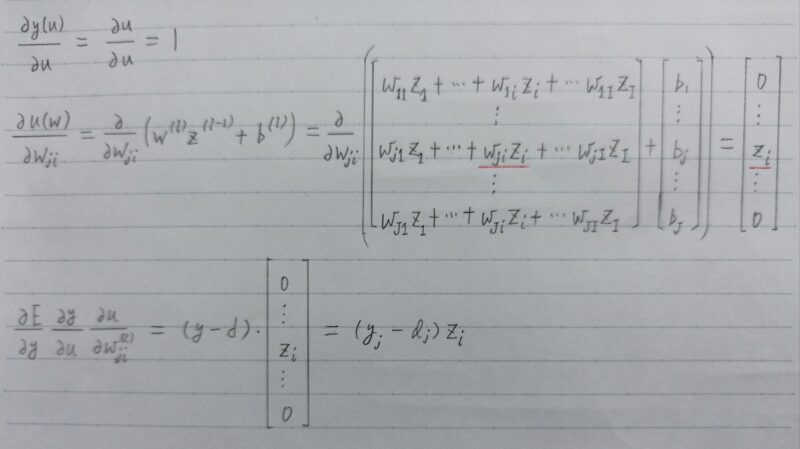
確認テスト
- Q1.誤差逆伝播法では不要な再帰的処理を避ける事が出来る。
既に行った計算結果を保持しているソースコードを抽出せよ。
A1.# 出力層でのデルタdelta2 = functions.d_mean_squared_error(d, y)
## 試してみようdelta1 = np.dot(delta2, W2.T) * functions.d_sigmoid(z1) - Q2.下記のソースコードを探せ
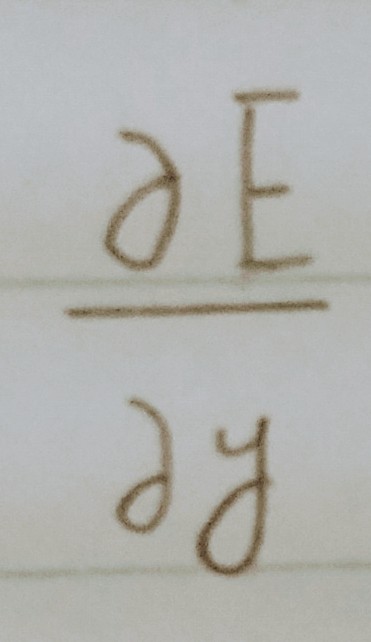
微分
↑
delta2 = functions.d_mean_squared_error(d, y)
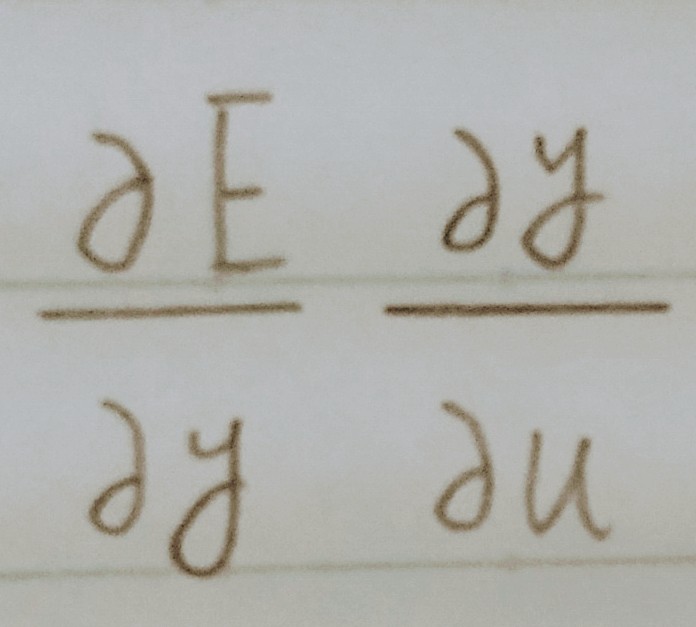
↑
delta2 = functions.d_mean_squared_error(d, y)
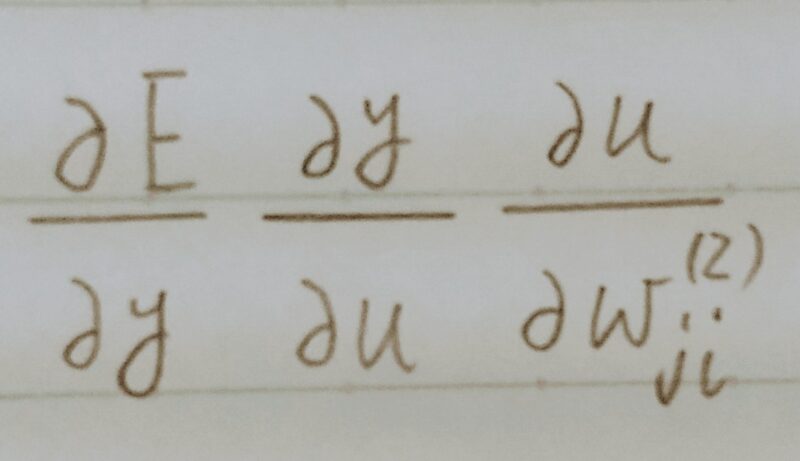
↑
grad[‘W1’] = np.dot(x.T, delta1)
ディープラーニングの開発環境
ローカルな開発環境(家にあるパソコン)
- どんなPCにも入っている→どんな処理にも使える
- 複数命令列・複数データ(MIMD:Multiple Instraction, Multiple Data)
- マルチコアCPU・・・複数のCPUをもつ。かつては1つのコアが一般的であったが、2007年頃から2つのコアが普及。4つのコアを持つものもある。
- 用途:ゲームPC
単一命令列・複数データ(SIMD:Single Instraction, Multiple Data)
の処理の性能を追求
当初はグラフィックを表示 ⇒ 汎用的な科学計算 - メモリにデータとプログラムを内蔵しメモリから命令を逐次取り出し
実行する ⇒ノイマン型プロセッサの一種
ハイエンドモデルは数千個の演算コアを持つ - Tensorflow や PyTorch にサポートされている。
- Field Programmable Gate Array・・・自分でプログラムできる計算機
ディープラーニングにおける行列演算を論理回路によって物理的に実装
⇒ 処理速度の高速化、低消費電力化 - 製造後に内部の論理回路の構成を書き換えることができる。
⇒ 柔軟な開発ができる - C/C++ や Python などの高級言語により回路を記述する。
⇒ その動作を実装するデジタルハードウェアを作成する
高位合成ツールを利用して開発を進める。
- プログラムできない計算機
ディープラーニングの演算に適した新しいプロセッサ
⇒ 行列演算に特化 - 数千の積和演算器が配置され、それらが直接接続されている。
⇒ このアーキテクチャ(=システムの概略構造あるいは基本的な骨組み)をシストリックアレイという。 - 演算結果を次の乗算器に渡す(メモリではない)
⇒ メモリアクセスの必要を無くし、スループットを向上
演算器の計算精度を 8 bit や 16 bit のみにする
⇒ スループットを向上、低消費電力化 - 例:TPUなど・・・
TPU・・・Googleが開発したディープラーニング専用(行列演算)の計算処理装置
CPU < GPU < FPGA < ASIC(TPU)
(遅い) ←ーーーーーーーーーーーー→(速い)
クラウド
- データセンター ← 間借り
- クラウドの例
AWS(Amazon Web Services)
GCP(Google Cloud Platform)
入力層の設計
- 連続する実数
- 確率
- フラグ値
例)[0, 0, 1] ← このような表現をoneーhotベクトル
犬 犬 猫
- 欠損値が多いデータ
- 誤差の大きいデータ
- 出力そのもの、出力を加工した情報
- 連続性の無いデータ(背番号とか)
- 無意味な数が割り当てられているデータ
・悪い例 Yes:1,No:0, どちらでもない:-1, 無回答:-1
・良い例 Yes:1,No:-1, どちらでもない:0, 無回答:なし
↑ one-hotベクトルで表現した方がよい
- 欠損値の扱い
ゼロで詰める(ただし・・・)
欠損値を含む集合を除く
入力として採用しない - データの結合
- 数値の正規化・正則化
過学習
- 訓練誤差とテスト誤差の差が大きくなる。
↓ - 過学習を防ぐ手法
・ドロップアウト
・正則化
ランダムにノードを削除して学習させる。
- 学習の過程において、大きな重みを持つことにペナルティを課すことで、過学習を抑制する。
L = E + 1/2 λ Σk(wk)2
L:損失関数
E:誤差関数
λ:正則化パラメータ
W:重み - L2正則化の場合 ← 荷重減衰(weight decay)という
dL/dw=dE/dwi+λwi ← 損失関数Lをパラメータwで偏微分 - L1正則化の場合
dL/dw=dE/dwi+λsgn(wi) ← 損失関数Lをパラメータwで偏微分
データ集合の拡張
- 学習データが不足するときに人工的にデータを作り水増しする手法
- 適性
分類タスク(画像認識)に効果が高い。 - 手法
・画像でのデータ拡張手法は様々なものが存在
例)オフセット、ノイズ、ぼかし、回転
・様々な変換を組み合わせて水増しデータを生成 - 注意点
データ拡張の結果、データセット内で混同するデータが発生しないよう注意
例)6と9など
- ノイズ注入によるデータ拡張
中間層へのノイズ注入で様々な抽象化レベルでのデータ拡張が可能 - データ拡張の適用
データ拡張の効果とモデル性能かの見極めが重要 - データ拡張の効果と性能評価
・データ拡張を行うとしばしば劇的に汎化性能が向上する。
・ランダムなデータ拡張を行う時は学習データが毎度異なるため再現性に注意。
- 一般的に適用可能なデータ拡張(ノイズ付加など)はモデルの一部として捉える(ドロップアウトなど)。
- 特定の作業に対してのみ適用可能なデータ拡張(Crop(クロップ)など)は入力データの事前加工として捉える。
補足)Crop(クロップ)とは画像の一部を取り出すこと
例:不良品検知の画像識別モデルに製品の一部だけが拡大された画像は入力されない。
転移学習(特徴量の転移)
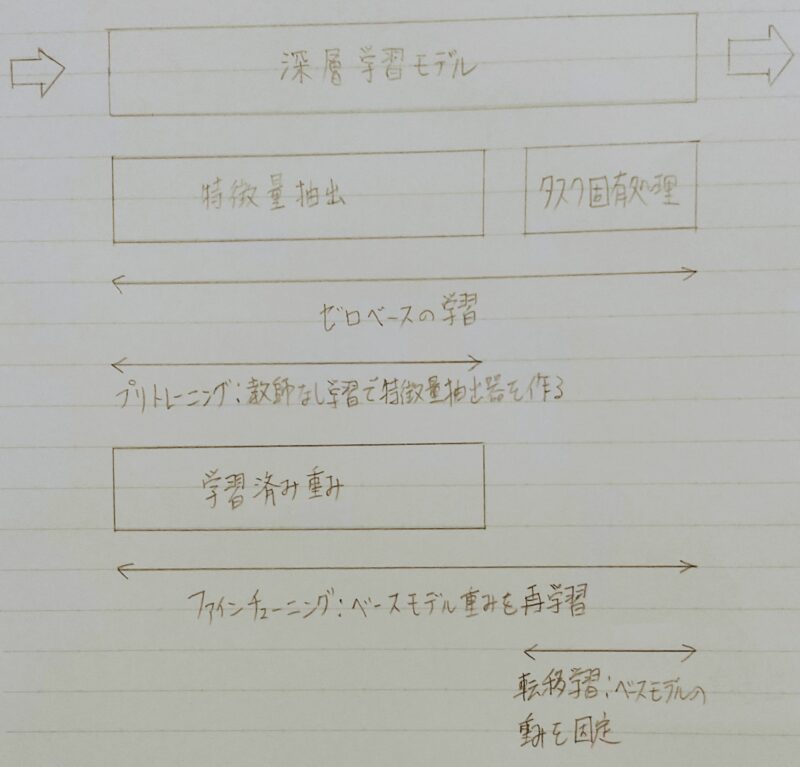
プリトレーニング:教師なし学習で行う。

「プレトレーニング」は非常に重要だよ!!

ファインチューニングの活用例:Wide ResNet(画像処理)、BERT(自然言語処理)
転移学習の活用例:VGG(画像処理)、GPT(自然言語処理)
- ワンショット学習:
1つの事例(データ)しか見ずに学習を行う(新たなデータに対して適切に分類できるようにする)ことである。
⇒ 他の転移学習と比較して大量の訓練データを必要としない。 - ドメイン適応:
対応ドメインの汎化性能を向上させる
⇒ 事前訓練済みパラメータ+対象ドメインの訓練データ
機械学習モデルのデバッグ
機械学習モデルをデバッグ
⇒ 定量的な評価値を確認 + 画像の出力データを可視化して確認
ドメインシフト
模擬演習問題
- Q1.以下の【図1】のような掛け算ユニットがある計算グラフで逆伝播を行ったとき、赤枠に当てはまる数字はどれか。次の選択肢の中から選びなさい。 なお、計算グラフは、計算の過程をグラフによって表したものであり、×は乗算を、+は加算を表している。
1.60
2.600
3.100
4.30000
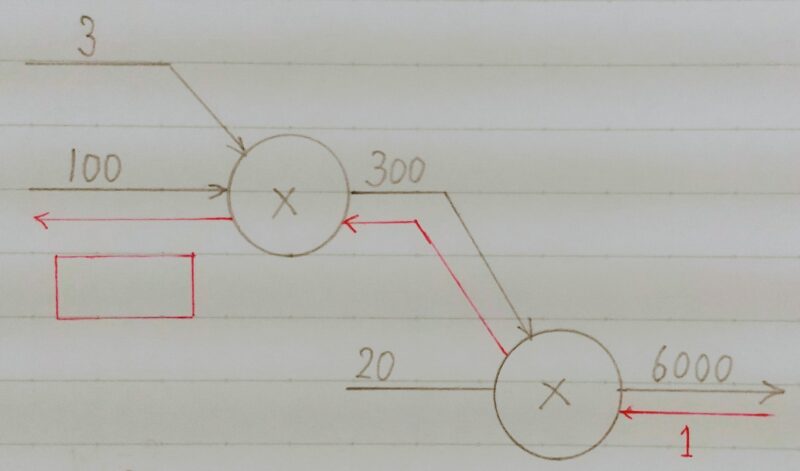
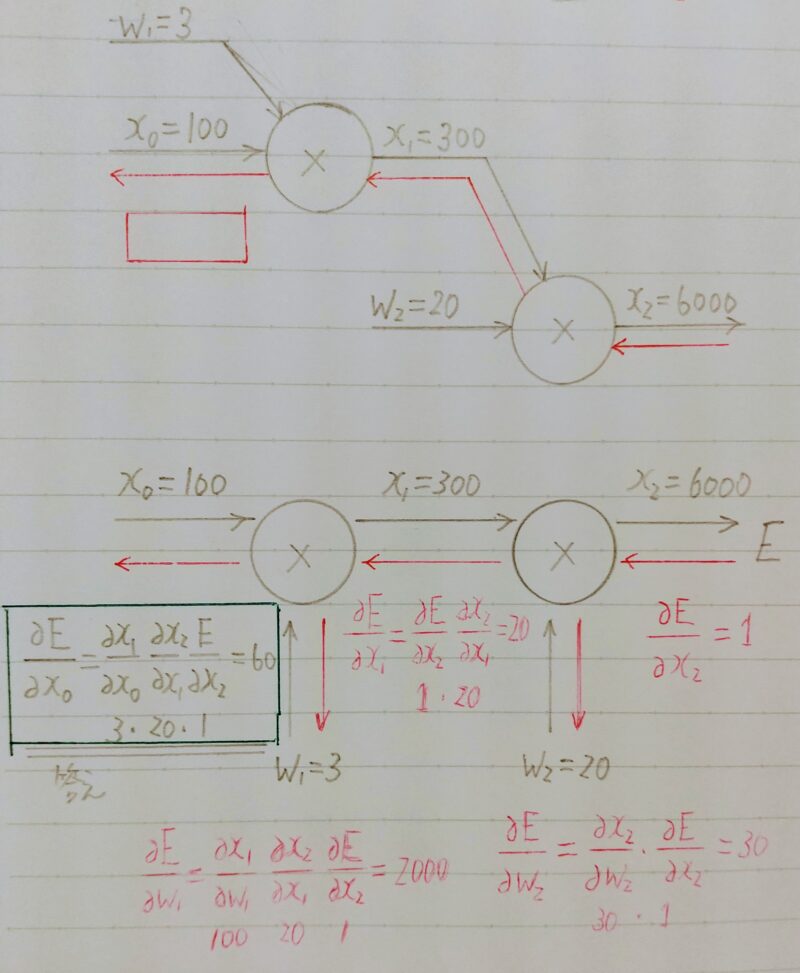
- A1.
- Q2.クラス分類とは、与えられた入力空間を相違なるK個の空間に分割し、それぞれの空間をクラスCkとラベルを付けることである。訓練データxが与えられた時に、推論段階と決定段階を経て各クラスに割り当てる。訓練データからどのようにして分類するかによって、生成モデル・識別モデル・識別関数に分けられる。
生成モデルではあるデータxについて、各Ciにおけるxとなる確率、すなわちp(x|Ci)とCiが出現する確率p(Ci)を求めることで、xがあるCiに分類される確率を求める。あるxiについて3つのクラスに分けたい。
P(xi|C0)=0.1、p(xi|C1)=0.3、p(xi|C2)=0.2、p(C0)=0.7、p(C1)=0.2、p(C2)=0.1であるときにxiがC1に属する確率を求めよ。
- A2.
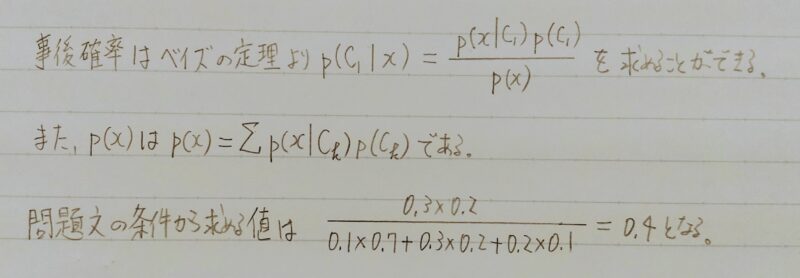
- Q3.識別モデルでは直接、事後確率p(Ck|x)を決める推論問題を解く。複数の球が入った箱があり、球の色が白か赤、大きさは大きいものと小さいものがある。球の数の分布が次のような表の様になっていることが分かっている。
このときp(Ck=白|x=大)を求めよ。ただし、Ckは白か赤の二値、xは”大”と”小”の二値しかとらないものとする。
| 大 | 小 | 計 | |
|---|---|---|---|
| 白 | 12個 | 28個 | 40個 |
| 赤 | 18個 | 4個 | 22個 |
| 計 | 30個 | 32個 | 62個 |
- A3.条件付確率の問題。p(Ck=白|x=大)は球の大きさが大きい時に色が白である確率である。 球が大きい場合、白が12個、赤が18個であることが分かっているので求める確率は、12/(12+18)=0.4である。
- Q4.未知のデータに対する性能(汎化性能)を評価することで、モデルの性能を正しく検証することができる。kー分割検証法でモデルの性能を検証したい。「データをk個に分割し、分割したk個の各データセットを学習に回す(k回学習を繰り返す)」という手順を1回行うことを1epochとする。
k=10、epoch=10のとき、評価の計算を行う回数は何回か。
ただし、1回の学習で1回の評価を行うものとする。 - A4.10[k]×10[epoch]=100
- Q5.以下の文章を読み、次の問題に答えよ。未知のデータに対する性能(汎化性能)を評価する事で、モデルの性能を正しく検証する事が出来る。検証法には様々な種類があるが、kー分割検証法の利点は何か。
適当なものを選択肢の中から1つ選びなさい。
1.計算時間が比較的短い。
2.他の手法と比べて、とても優れた性能を発揮するモデルの学習を行うのに有効な手法である。
3.サイズの小さいデータセットを活用して、繰り返し学習と評価を行うことで、過学習を防ぐ。
4.データセットのサイズが大きいとき、効率よく学習を行う。 - A5.正解は3である。 kー分割検証法はサイズの小さいデータセットの場合に、精度を高めることのできる手法である。
ただし、繰り返し学習と評価を行うため、計算時間がかかるという欠点がある。
- Q6.確率は身の回りの様々な場所で用いられている。例えば、自動運転の分野では自分の位置を推定するために用いられている。確率の計算を行うにあたって、基になっているものにベイズの定理がある。 ベイズの定理を構成する要素として誤っているものはどれか。選択肢の中から1つ選びなさい。
なお、Aは事象aの確率変数を、Bは事象bの確率変数を表す。
1.p(A)は事象aが起こる確率を表す。
2.p(B)は事象bが起こる確率を表す。
3.p(A|B)は事象aが起こるという条件のもとで事象bが起こる確率を表す。
4.p(B|A)は事象aが起こるという条件のもとで事象bが起こる確率を表す。 - A6.正解は3である。
p(A|B)は事象bが起こるという条件のもとで事象aが起こる確率を表す。


コメント
コメント一覧 (9件)
カード型フォーマット 細部までこだわり — 情報が濃縮。
こんにちは。瑞島 魁祐です。コメントありがとうございます。投稿の励みになります。
特別に感謝 週末ルート紹介。
こんにちは!「瑞島 魁祐(みずしま かいゆう)」です。コメントありがとうございます。投稿の励みになります。
新ルート&レポ期待。
こんにちは!!
コメント頂き有難うございます。
投稿の励みになります。
あなたのブログ見ていると、よくわかります、旅行って本当に元気が出ること。本当に感謝! 勝手に笑顔になるありがとう! [url=https://iqvel.com/ja/a/%E3%83%99%E3%83%AB%E3%82%AE%E3%83%BC/%E3%82%AD%E3%83%AA%E3%82%B9%E3%83%88%E3%81%AE%E8%81%96%E8%A1%80%E6%95%99%E4%BC%9A]二層の聖堂[/url] 移動目安助かる — サステナブルな旅実現する。
こんにちは!!
コメント頂きましてありがとうございます。
投稿の励みになります。
楽しく見てます。すごい写真もいいですね。 [url=https://iqvel.com/ja/a/%E3%82%A4%E3%82%B9%E3%83%A9%E3%82%A8%E3%83%AB/%E6%B6%99%E3%81%AE%E5%A3%81]西壁[/url] ガイド系に大感謝!