- 「サポートベクターマシン」について学びたいけど理解できるか不安・・・
- 「サポートベクターマシン」についてどこから学んでいいか分からない?
- 「サポートベクターマシン」を体系的に教えて!
「サポートベクターマシン(SVM:Support Vector Machine)」1990年代に提案され、2000年代前半に急速に発展した手法です。汎化性能が高く、応用分野が広いものでデータ分析の現場において近年最も注目を集めているモデルですが、興味があっても理解できないケースは非常に多いです。
私は過去に基本情報技術者試験(旧:第二種情報処理技術者試験)に合格し、また2年程前に「一般社団法人 日本ディープラーニング協会」が主催の「G検定試験」に合格しました。現在、「E資格」にチャレンジ中ですが3回不合格になり、この経験から学習の要点について学ぶ機会がありました。
そこでこの記事では、「サポートベクターマシン」を学習する際のポイントについて解説します。
この記事を参考に「サポートベクターマシン」が理解できれば、E資格に合格できるはずです。
<<「サポートベクターマシン」のポイントを今すぐ見たい方はこちら
目次
概要
サポートベクターマシン(SVM)とは・・・
- 1990年代に提案され、2000年代前半に急速に発展した手法
- 汎化性能が高い(=応用分野が広い)
- データ分析の現場において近年最も注目を集めているモデル
クラス分類
クラス分類とは・・・
- 教師あり学習
- 基本的に2クラス分類問題に特化している
補足)2クラス問題とは「与えられた入力データが2つのカテゴリーのどちらかに属するかを識別する問題」
決定関数と分類境界
決定関数
- データ点xを下式の正負によって分類する。
- y(x)=wTφ(x)+b
φ(x):特徴ベクトル(feature vector)(または入力ベクトル(input vector)と呼ぶ) - y:ラベル(label)
分類境界
- サポートベクトル・・・境界線(面)の最も近くにあるデータ点(マージン上にある)をいう。
補足)サポートの由来はサポートベクトルが境界線(面)を「支えている」ことから来ている様。 - ※サポートベクターマシン(SVM)・・・マージンの外側のデータは予測に影響を与えない
線形サポートベクトル分類
ハードマージン
線形サポートベクトル分類(ハードマージン)
- マージン・・・判別する境界とデータ(=サポートベクトル)との距離 ← 最大化
- カーネル・・・2つのベクトル xx と yy の内積を特徴空間で計算する方法
ソフトマージン
線形サポートベクトル分類(ソフトマージン)
- 次の目的関数を最小化する。
C Σ ξi + 1/2||W||2
ξ:スラック変数・・・データ点xiがマージン内または誤分類されたときに正の値をとる
C:正規化係数・・・正の定数でこの値を大きくすることでξiの増加に対しより強いペナルティを与える。
- C → ∞にしていくと・・・
・マージン内に訓練データが入ることや誤分類を一切許容しない。(=ハードマージンSVMと同じ)
・Cが大きい方が訓練時の正解率が高くなるが過学習に陥っている可能性がありテスト時の正解率が高くなるとは限らない。 - C → 0にしていくと・・・
・ξiの値が増えても目的関数の値はそれほど増加しないため、より誤分類が許容されやすくなる。
・一般に過学習を防ぐためには誤分類をある程度許容した方がよいためCを小さくする方がよい。
カーネルトリックとは・・・
背景
- サポートベクターマシン(SVM)で非線形問題を扱う場合
射影関数φを使って線形分離できないデータを高次元の特徴空間に変換し、線形分離可能とする。 - 特徴空間が高次元であるほど計算コストが高くなる。
- カーネルトリックを使用する目的:計算コストを抑える対策
カーネルトリックの種類
- 正規化線形カーネル
k(x,x´)=xTx´/(||x|| ||x’||)
特徴ベクトル φ(x) = x/||x||
※カーネル=特徴ベクトルの内積 - 線形カーネル
k(xi,yi) = kxiTyi + b - ガウス動径基底関数(Gaussian)カーネル(=RBFカーネル(Radial basis function Kernel))
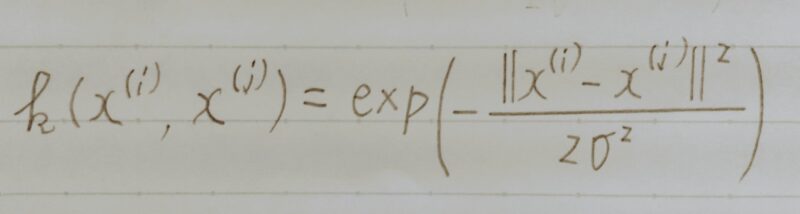
上式はカーネル関数の一つでサポートベクターマシン(SVM)など内積のみを扱う線形のアルゴリズムを非線形化する際に登場する。
- 多項式カーネル
2つの同じサイズのベクトルx,yを入力とし、スカラーを返す以下のような関数k(x,y)を、多項式カーネルという。
k(x, y) = (1 + xTy)d
(次数dは正の整数とする) - シグモイドカーネル
K(xi,xj) = tanh(bxiTxj + c)
カーネル関数の特徴
- 一般にカーネル関数は暗に高次元の「特徴空間」へ写像することを意味する。
・モデルの表現力が上がる。
・内積計算を回避することができる。 - マージンの外側のデータは予測に影響を与えない。
(識別では決定境界から最も近いデータが予測に利用される。) - カーネルはある特徴ベクトルφ(x)の内積として定義される。
カーネルトリックの応用例
- 識別モデル:〈特徴〉 低次元→高次元、学習データ多い 、画像認識
- 生成モデル:隠れマルコフモデル、ベイジアンネットワーク、変分オートエンコーダー(VAE)、敵対的生成ネットワーク(GAN)、画像生成、テキスト生成
SVMにおける双対表現
編集中
極値問題/偏微分
編集中
双対問題の導出
- ラグランジュ(Lagrangue)関数
- 主変数(primal variable)
- 双対変数(dual variabule)
主問題と双対問題の関係
- 弱双対性
- 強双対性
カーネルを用いた非線形分類への拡張
- 写像
- カーネル関数
まとめ
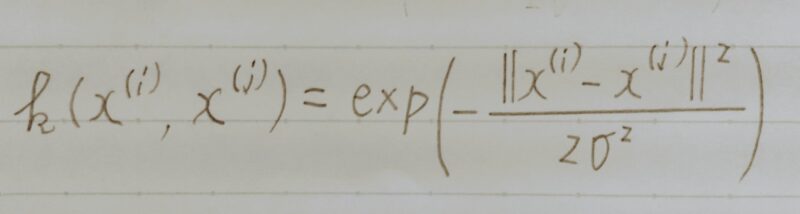
最後まで読んで頂きありがとうございます。
皆様のキャリアアップを応援しています!!

コメント