- 「AI(人工知能)モデルを構築する方法」について学びたいけど理解できるか不安・・・
- 「AI(人工知能)モデルを構築する方法」についてどこから学んでいいか分からない?
- 「AI(人工知能)モデルを構築する方法」を体系的に教えて!
AI(人工知能)モデルを構築するには、①レイヤー層(入力層、隠れ層、出力層)、②活性化関数、③損失関数(=誤差関数=目的関数)、④最適化手法、⑤オーバーフィッティング対策などを決定しなければならないですが、難しそうで何から学んだらよいか分からないケースは非常に多いです。
私は過去に基本情報技術者試験(旧:第二種情報処理技術者試験)に合格し、また2年程前に「一般社団法人 日本ディープラーニング協会」が主催の「G検定試験」に合格し、現在、「E資格」取得にチャレンジ中ですが、人工知能の勉強を始めた頃は多くの考え方や専門用語に圧倒され、全貌を理解するのに苦労した苦い経験があります。
そこでこの記事では、AIモデルを構築する方法について説明します。
この記事を参考にして「AI(人工知能)モデルを構築する方法」が理解できれば、G検定に合格できるはずです。
<<「AI(人工知能)モデルを構築する方法」のポイントについて今すぐ見たい方はこちら
AIモデルの概要
説明の前にどのようなAIモデルを構築するか概要を説明する。AIモデルを決定するためには次の①~⑤の項目を設定する必要がある。
- ①レイヤー層(入力層、隠れ層、出力層)
- ②活性化関数
- ③損失関数(=誤差関数=目的関数)
- ④最適化手法
- ⑤オーバーフィッティング対策
①~⑤について順番に説明する。ただし、説明の前にどのようなAIモデルを構築するか概要を説明する。
まず、AIモデルの概要について説明する。AIができる機械学習には下表のとおり教師あり学習、強化学習、教師なし学習がある。ここで取り扱う問題は教師あり学習の中の「回帰問題」と「分類問題」とする。
例:

〈回帰問題〉後日、追記予定。
〈分類問題〉入力データ(2次元)に対して出力データ(1次元)を返すAIモデルを考える。
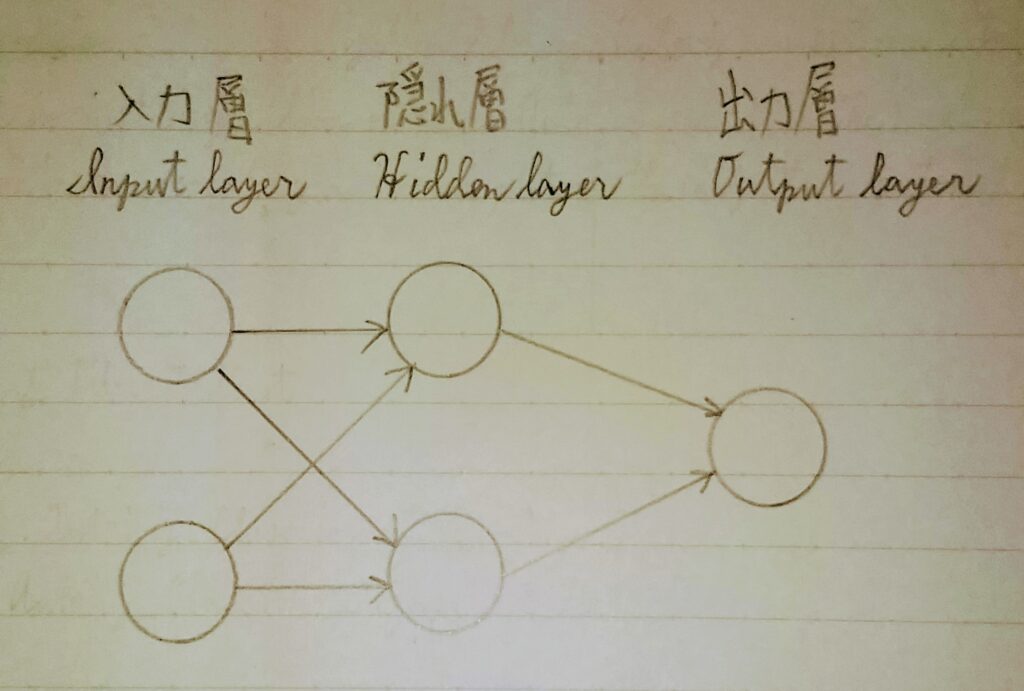
上記のAIモデルを数式に表すと y = w1x1 + w2x2 + b ・・・①
- ※1 x1、x2:入力値
- ※2 y:出力値
- ※3 w1、w2:入力xに係る重み
- ※4 b:バイアス
x1、x2、yは訓練データより与えられるため、 x1、x2とyの関係があうようにw1、w2、bの値を決定するのがAIモデルを学習する目的である。
ここで、上記①のAIモデルを利用できる場面を考えてみる。
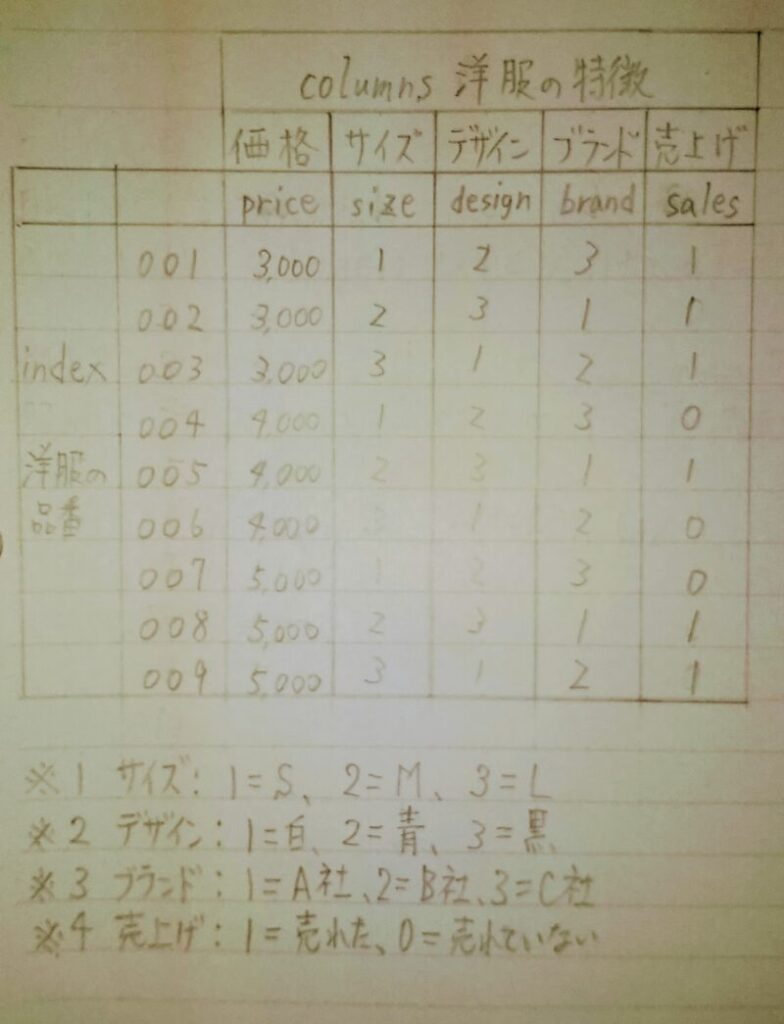
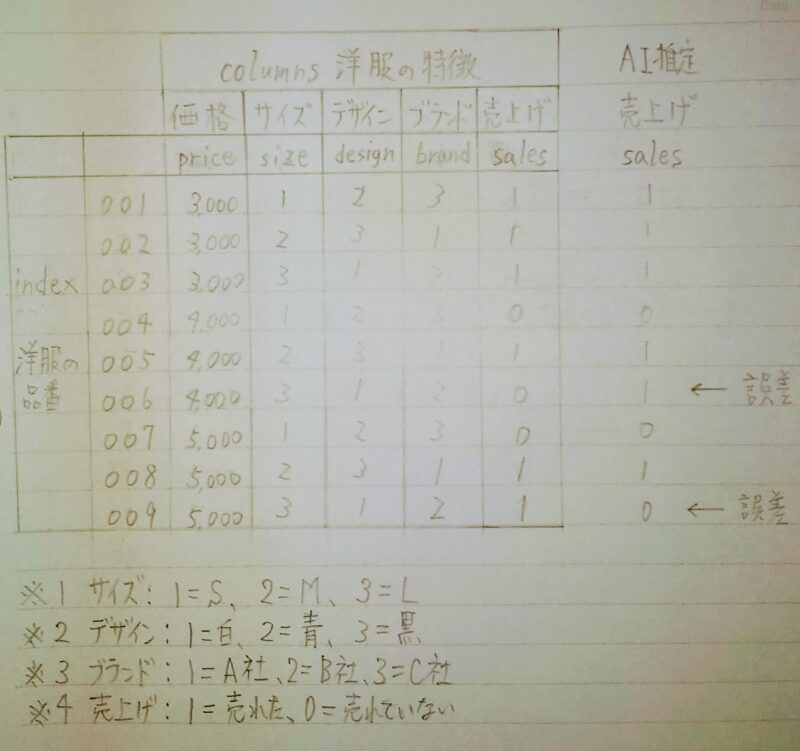
あなたは商品を売る面白さを感じて商売をしてお金を稼ぎたいと思ったことはないだろうか?例えばあなたが洋服の小売店の店主であったと仮定する。あなたは売上げを伸ばしたいが、出来るだけ在庫を抱えたくないと思った。このため、仕入れに際して「売れる確率の高い洋服を仕入れる」ため過去の販売実績(下表)を参考にしようと考えた。ここでAIが活用できる場面が訪れたのである。過去の販売実績データがあれば売れる確率の高い洋服をAIに推定させることができる。
洋服が売れる原因には、下表のように価格、サイズ、デザイン、ブランド等があるが、ここでは問題を単純にするため「価格」と「サイズ」のみを原因とする。
ここで上記のAIモデルを数式に今回の例に具体的に落とし込んでみる。 y = w1x1 + w2x2 + b ・・・①
- ※1 x1:入力値1 ← 価格
- ※2 x2:入力値 ← サイズ
- ※3 y:出力値 ← 売上げの有無
- ※4 w1:入力値1(価格)に係る重み
- ※5 w2:入力値2(価格)に係る重み
- ※6 b:バイアス
上記の様に洋服が売れるか売れないかを推定する問題はAIで扱う「2値分類」問題に置き換えることができる。
上記のAIモデルをコード化すると下記のようになる。
import torch import torch.nn as nn import torch.nn.functional as F
# 入力層、隠れ層、出力層のユニット数を定義
n_input = 2 # 入力層のユニット数:2 n_hidden = 2 # 隠れ層(中間層)のユニット数:2 n_output = 1 # 出力層のユニット数:1
# 活性化関数を定義
activation = torch.nn.ReLU() #入力層→隠れ層はReLU関数を用いる activation = torch.nn.Sigmoid() #隠れ層→出力層はシグモイド関数を用いる
# 「torch.nn.Moduleクラスのサブクラス化」によるAIモデルの定義
class NeuralNetwork(nn.Module):
def __init__(self): #__init__()の定義
super(NeuralNetwork, self).__init__() #親クラスのメソッドを呼び出す
self.layer1 = nn.Linear(n_input, hidden) # 層(layer:レイヤー)を定義
self.layer2 = nn.Linear(hidden, n_output) # 層(layer:レイヤー)を定義
def forward(self, input):
# フォワードパスを定義
output = activation(self.layer1(input)) # 活性化関数は変数として定義
# 「出力=活性化関数(第n層(入力))」の形式で記述。
# 層(layer)を重ねる場合は、同様の記述を続ける。
# 「出力(output)」は次の層(layer)への「入力(input)」に使う。
return output
# モデル(NeuralNetworkクラス)のインスタンス化
model = NeuralNetwork()
model # モデルの内容を出力
- ※1 torch:PyTorchのメインパッケージ
- ※2 nnパッケージ:ニューラルネットワーク( NeuralNetwork )機能
- ※3 nn.Linear( n_input, n_output ):入力データ(=n_input)を線形変換できるクラス
- ※4 サブクラス化:オブジェクト指向プログラミングにおいて、既存のクラスの機能や構造を継承して新しいクラスを作成することである。サブクラスは、子クラス、派生クラスとも呼ばれ、元となるクラスはスーパークラス、親クラス、基底クラスと呼ばれる。
- ※5 クラス:設計図のようなもので、オブジェクトを生成するために定義された概念。例えば自動車、飛行機、船は種類は違うが「乗り物」としての共通性(概念)を持っている。共通性(概念)をひとまとめにしたのがクラス。例でいえば「乗り物」がクラス。
- ※6 オブジェクト:設計図をもとに実体化したもの。上記の例では自動車、飛行機、船がオブジェクト
- ※7 実体化:クラスをインスタンス化(コンピュータがメモリを確保した状態)すること。
- ※8 オブジェクト指向:オブジェクト同士の相互作用として、システムの振る舞いをとらえる考え方
以降、上記コードの各項目を順番に解説する。
レイヤー層の定義
レイヤー層を定義する。torch.nn.Linearクラスはレイヤー(層)を定義しており「入力に対して 線形変換を行うこと」を意味し、一般には全結合層(Fully Connected Layer)と 呼ばれている。
〈回帰問題〉 例:後日、追記予定
〈分類問題〉 例: n_input = 2 # 入力層のユニット数:2 n_hidden = 2 # 隠れ層のユニット数:2
n_output = 1 # 出力層のユニット数:1 ・ ・ self.layer1 = nn.Linear( n_input , hidden) # 層(layer:レイヤー)を定義 self.layer2 = nn.Linear(hidden, n_output) # 層(layer:レイヤー)を定義
- ※1 Linearクラスのコンストラクター (厳密には__init__関数)の第1引数と第2引数には、入力ユニット数と出力ユニット数を指定すればよい。
- ※2 n_input:学習データの入力ユニット数。AIモデルへ入力する学習データの次元数を決めるもので出力結果に影響がありそうな要素を選定する。
- ※3 n_hidden :隠れ層のユニット数。入力に対する隠れ層の次元数を決定する。今回は2つの入力項目に対して2種類に分類するAIモデルなので隠れ層の次元数は2とする。
- ※4 n_output :出力ユニット数。入力に対する出力の次元数を決定する。今回は2つの入力項目に対して2種類に分類するAIモデルなので出力次元数は1とする。
活性化関数
AIモデルへのデータ入力に対してどのような出力になるか応答の仕方を決めるものである。図に示すと下図のとおりである。
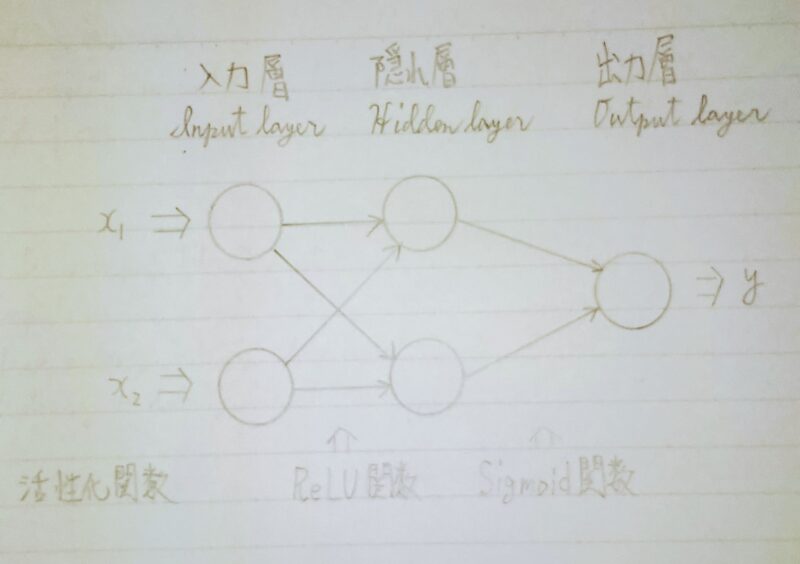
〈回帰問題〉 例:後日、追記予定 〈分類問題〉 ノードの途中の場合と最後のノードの場合では異なる。 入力層→隠れ層:ReLU関数 (一般にReLU関数が用いられる) 隠れ層→出力層:シグモイド関数 (一般に2値分類にはシグモイド関数が用いられる)
activation = torch.nn.ReLU() #活性化関数(ReLU)を変数(activation)として定義する hidden = activation(self.layer1(input))
activation = torch.nn.Sigmoid() #活性化関数(Sigmoid)を変数( activation )として定義する output = activation(self.layer2(hidden))
- ※1 ReLU(Rectified Linear Unit、「レルー」と読む):隠れ層によく使用される関数。
- ※2 Sigmoid(シグモイド):出力層(2値分類)によく使用される関数。
- ※3 〈参考〉ソフトマックス関数:出力層 (多値分類)によく使用される関数。
損失関数(=誤差関数=目的関数)
(出力、目標)入力のペアを受け取り、出力が目標からどれだけ離れているかを計算する。損失関数には様々な種類がある。
回帰問題に使用される損失関数
回帰問題に使用する損失関数の例を下記に示す。MSE(Mean Absolute Error:平均絶対誤差)、RMSE(Root Mean Squared Error:二乗平均平方根誤差)、RMSLE(Root Mean Squared Logarithmic error:二乗平均平方根対数誤差)は回帰問題によく使用される。

例: criterion = nn.L1Loss() #MSE(Mean Absolute Error:平均絶対誤差) criterion = nn.MSELoss() #RMSE(Root Mean Squared Error:二乗平均平方根誤差)
- ※1 criterion:基準
- ※2 nnパッケージ:いくつかの異なる損失関数がある。
分類問題
分類問題には二値分類と多項分類がある。以下に各々の分類問題に使用する損失関数の例を示す。
二値分類
2値分類によく使用される損失関数には、binary_cross_entropy(バイナリークロスエントロピー)やlogit_binary_cross_entropy(ロジット・バイナリ交差エントロピー)などがある。

例: criterion = nn.BCELoss() #binary_cross_entropy(バイナリ交差エントロピー) criterion = nn.BCEWithLogitsLoss() #logit_binary_cross_entropy(ロジット・バイナリ交差エントロピー) ※1 nnパッケージ:いくつかの異なる損失関数がある。 ※2 logit_binary_cross_entropy(ロジット・バイナリ交差エントロピー) は バイナリ交差エントロピー 損失に最初からシグモイド関数が加えられたもの
多項分類
softmax_cross_entropy(ソフトマックスクロスエントロピー)は多項分類問題によく使用される損失関数である。

例: criterion = nn.CrossEntropyLoss() # ソフトマックス交差エントロピー criterion = nn.functional.nll_loss() # 負の対数尤度損失_nll_loss関数 criterion = nn.NLLloss() # 負の対数尤度損失_NLLLossクラス
※nnパッケージ:いくつかの異なる損失関数がある。
最適化手法
下記の①式の「重み」(=w1、w2)を最適化する。重みを最適化するとは誤差(上記の損失関数)が最小になるような重みを探索することである。最適化手法には以下のものがある。
上記のAIモデルを数式に表すと y = w1x1 + w2x2 + b ・・・①
※1 x1、x2:入力値 ※2 y:出力値 ※3 w1、w2:入力xに係る重み ※4 b:バイアス
例: optimizer=optim.SGD(net.parameters(), lr=0.01) ♯ 確率的勾配降下法 optimizer=optim.Adagrad(net.parameters(), lr) ♯ Adagrad optimizer=optim.RMSprop(net.parameters(), lr) ♯ RMSprop optimizer=optim.Adadelta(net.parameters(), lr) ♯ Adadelta optimizer=optim.Adam(net.parameters(), lr) ♯ Adam optimizer=optim.AdamW(net.parameters(), lr) ♯ AdamW
- ※1 SGD(Stochastic Gradient Decent):確率的勾配降下法といい代表的な最適化手法であり、求めた勾配方向にその大きさだけパラメータを更新する方法
- ※2 Adagrad(Adaptive Gradient Algorithm):学習率を学習過程の中で更新していく方法。パラメータの更新度合いにより、次の学習率を各パラメータ毎に調整する。すなわち、大きく更新されたパラメータの学習率は、より小さく調整される。そのため、大きな勾配の影響が小さくなり、効率的に最適化を行うことができる。全ての勾配情報を記憶して いくため、学習が進んでいくと同時に学習率が小さくなる。最小値がさらに先にある場合、勾配があっても更新量が小さく更新されにくくなってしまう。
- ※3 RMSprop(Root Mean Square propagation):「Adagrad」の問題点を受けて提案されたものになる。「RMSprop」では勾配情報の記憶を行うが、古い情報を落として、新しい勾配情報がより反映されるように記憶していきます。これにより、学習が進んでいっても、その場での勾配情報を反映し、学習率の調整を適切に行うことができる。
- ※4 Adadelta:単位が整うように「Adagrad」や「RMSprop」を改良したもの。上記の最適化手法は、基本的に単位が整っていない。勾配とパラメータでは単位が異なっているが、更新式の中で単位の違いは特に考慮されず計算されていない。そのため結果的に、パラメータを勾配の単位で更新するということになる。特徴として学習率の設定が不要となる
- ※5 Adam(Adaptive Moment Estimation):「Momentum」と「Adagrad」の融合というアイディアにより考案された。「Momentum」のようにボールが転がるような動きをするが、学習率を調整していくので、徐々に振れ幅は小さくなり、ゼロに近づいていく。
- ※6 AdamW:「Adam」の Weight decay(重み減衰)に関する式について変更を行ったもの。損失関数計算時およびパラメータ更新時において、L2 正則化項を追加することで、「Adam」よりも適切な Weight decay を得ることを目的としている。
- ※7 lr:学習率、SGDは0.01、それ以外は1に設定
誤差逆伝播
誤差(=損失関数の値)」が最小になるような重みを求める。具体的には横軸に重み、縦軸に誤差とした最適化手法の関数の勾配が0になるような重み(パラメータ)の値を求める。そして、その重みをAIモデルへ代入する。
例: optimizer.zero_grad() #オプティマイザーで計算した勾配が累積するため初期化する output=net(input) #input(入力値)をAIモデルへ代入しoutput(出力値)を算出する loss = criterion(output, target) #output(出力された値)と目標値(target)から誤差を計算 loss.backward() #誤差逆伝播 optimaizer.step() #学習率と最適化手法に基づいて重みを更新
※1 torch.optim.Optimizer:Pytorchに用意されている最適化手法
オーバーフィッティング対策
過学習を防ぐために、学習の際にランダムにニューロンを「ドロップアウト」させる。
例:torch.nn.Dropout(p = 0.3, inplace = False)
※1 訓練中にp(=要素が0になる確率。デフォルト:0.5)からのサンプルを使用して、確率で入力テンソルの要素の一部をランダムに0にする。各チャネルは、転送呼び出しごとに個別に0になる。
まとめ
最後まで読んで頂きありがとうございます。
皆様のキャリアアップを応援しています!!
コメント