- 「GCN(グラフ畳み込み)」について学びたいけど理解できるか不安・・・
- 「GCN(グラフ畳み込み)」を使うメリットが分からない?
- 「GCN(グラフ畳み込み)」を体系的に教えて!
「GCN(Graph Convolutional Networks:グラフ畳み込み)」はグラフを入力した場合でも畳み込みできるネットワークで医療分野へ応用されている注目のディープラーニング手法ですが、興味があってもその内容の理解が難しいケースは非常に多いです。
私は過去に基本情報技術者試験(旧:第二種情報処理技術者試験)に合格し、また2年程前に「一般社団法人 日本ディープラーニング協会」が主催の「G検定試験」に合格しました。現在、「E資格」にチャレンジ中ですが3回不合格になり、この経験から学習の要点について学ぶ機会がありました。
そこでこの記事では、「GCN」を学習する際の3つのポイントを解説します。
この記事を参考にして「GCN」が理解できれば、E資格に合格できるはずです。
目次
1.「GCN」開発の背景
「GCN」開発の背景
〈復習〉畳み込みって何?
- そもそも何をしたい概念?
y(t)=g(t)・x(t)
もとの関数にフィルターをかける!
- 何のために?
⇒ 用途は様々!(だから概要をつかみにくい)
今回は特徴をはっきりさせるため
CNN(畳み込みニューラルネットワーク)の課題
- 畳み込みを画像やテキストに対して使う→ CNN(畳み込みニューラルネットワーク)
- CNNはグリッド構造がないため直接的にはグラフデータに用いることができない。
課題の解決策
畳み込みをグラフデータに対して行う手法→ GCN(Graph Convolutional Networks:グラフ畳み込み)
GCNの用途
- 新型コロナウイルス対策
(感染者の数を予測できるかもしれない)
2.「Spatial GCN」と「Spectral GCN」の比較
| Spatial GCN (空間的GCN) | Spectral GCN (スペクトルGCN) | |
|---|---|---|
| 概要 | ・グラフにクラスタリングを繰り返す。 ・クラスタリング:与えられたデータをk個のクラスに分類する。 | ・グラフラプラシアン行列Lを使用 ・対応するベクトルの組み合わせを見付け畳み込みをグラフ全体まで拡張。 ・グラフラプラシアン行列L:信号処理分野におけるフーリエ変換と同様の役割を果たす。 |
| メリット | 扱える幅が広い | 圧縮を効果的を行うことができる |
| デメリット | ・次元が低く近傍のある場所が限られる場合、広い範囲で重みを持たせにくい | ・計算量が多い⇒Lの固有値分解を含むため、最低でも O(N2)の計算量がかかる。下記「3.GCNの計算」参照。 ・パラメータ活用の制限 サイズと構造が変わるとパラメータの使い回しができない⇒ 異なる構造のグラフ間で同じパラメータを利用できない。(フィルターがグラフの固有基底に依存しているため) ・学習されるパラメータΘがQに依存(下記「3. GCNの計算」参照)→ 後にChebnet登場(GCNが空間領域に踏み込むきっかけに) |
3.GCNの計算方法
グラフ畳み込み演算*Gは、次のように定義される。
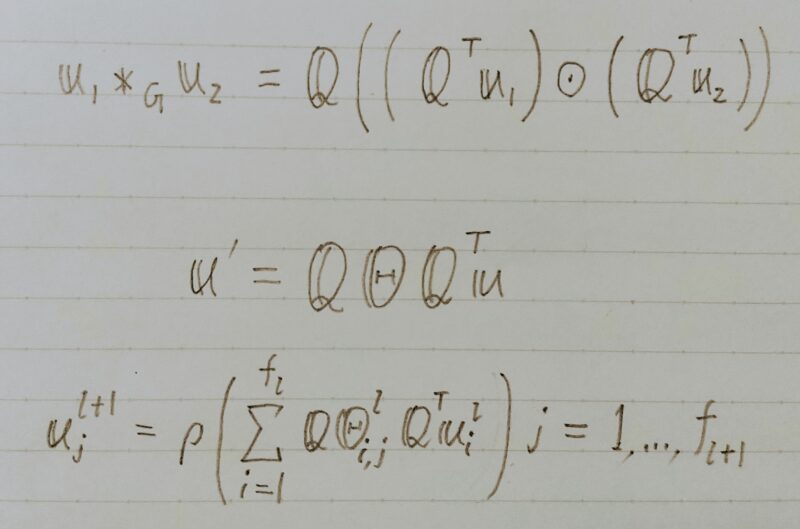
- u1:ノードで定義された信号
u2:ノードで定義された信号
Q:Lの固有ベクトル
Θ:学習されるパラメータ - 補足)⦿・・・アダマール積
4.まとめ
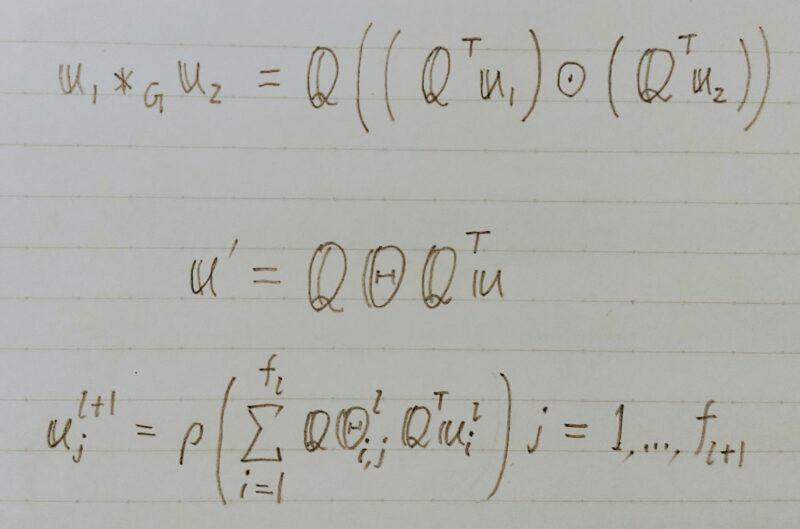
最後まで読んで頂きありがとうございます。
皆様のスキルアップを応援しています!!

コメント