- 「AI(人工知能)」を活用したいけど判断根拠が説明できないから不安・・・
- 「AI(人工知能)」の判断根拠をどのように説明できるのか分からない?
- 「AI(人工知能)」のブラックボックス性の解消方法を体系的に教えて!
「AI:Artificial intelligence,人工知能」は既に様々な商品・サービスに組み込まれて利活用が始まっている注目の技術ですが、AIを実社会に実装した後に「なぜ予測が当たっているのか」か分からないという不安が生じるケースがあります。
私は過去に基本情報技術者試験(旧:第二種情報処理技術者試験)に合格し、また2年程前に「一般社団法人 日本ディープラーニング協会」が主催の「G検定試験」に合格しました。現在、「E資格」にチャレンジ中ですが3回不合格になり、この経験から学習の要点について学ぶ機会がありました。
そこでこの記事では、AIの「判断根拠の説明方法」についてポイントを解説します。
この記事を参考にAIの「判断根拠の説明方法」が理解できれば、E資格に合格できるはずです。
<<AIの「判断根拠の説明方法」のポイントを今すぐ見たい方はコチラ
1.なぜ解釈性が重要なのか?

なぜAIモデルの解釈性が重要なのかなあ?

次の理由からだよ!!
- ディープラーニング活用の難しいことの1つは「ブラックボックス性」
- 判断根拠が説明できない
- 実社会に実装する後に不安が発生 「なぜ予測が当たっているのか」を説明できない
例:「AIによる医療診断の結果、腫瘍は悪性ですが、AIがそう判断した根拠は解明できません」と言われたらどんな気持ちになるか想像してみてください。 - モデルの解釈性に注目し、「ブラックボックス性」の解消を目指した研究が進められている
- CAM
- GradーCAM
- LIME
- SHAP
2.CAM
- Class Activation Mapping
- 提案論文:Learning Deep Features for Discriminative Localization
- 論文の概要
・GAP(Global Average Pooling)の再検討
・GAPは学習の過学習を防ぐ、正則化の役割として使われてきた
・GAP⇒CNN(畳み込みニューラルネットワーク)が潜在的に注目している部分を可視化できるようにする役割
- ネットワークの大部分が畳み込み層で構成されている
- 最終的な出力層の前にGAPを実行している
〈直感的〉出力層の重みを畳み込み特徴マップに投影する⇒ 画像領域の重要性を識別する
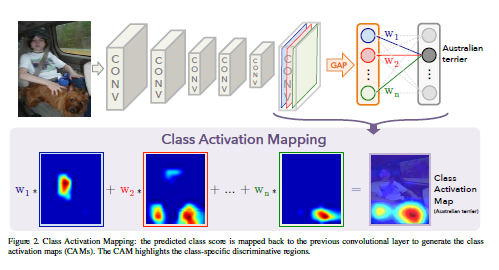
引用元:Learning Deep Features for Discriminative Localization
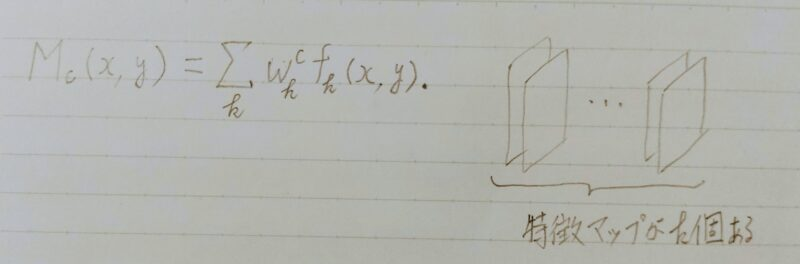
- Mc(x、y):どこに注目しているかを示すマップ
(x、y)が特徴マップの座標、fkが最後の畳み込み層のチャンネルのうちk番目の特徴マップ - Wck:出力クラスCにつながる重み
- CAMの評価:CAMの精度を確認するために、CAMの結果からバウンディングボックスを生成し、物体検出の評価指標を使い精度を比較している(Localization)
- GoogleNetーGAPはLocalizationで一番低いエラー率を達成している
3.GradーCAM
- CNNモデルに判断根拠を持たせ、モデルの予測根拠を可視化する手法
名称の由来は”Gradient”=「勾配情報」 - 最後の畳み込み層の予測クラスの出力値に対する勾配を使用
- 勾配が大きいピクセルに重みを増やす(=予測クラスの出力に大きく影響する重要な場所)

- αkC:クラスcのk番目のフィルタに関する重み係数
↑ この重み係数が大きいほど特徴マップkがクラスcにとって重要 - yc:クラスcのスコア
- Akij:k番目の特徴マップの座標(i,j)における値
- ycのAkにおける勾配を、特徴マップの全要素について Global Average Pooling を施す
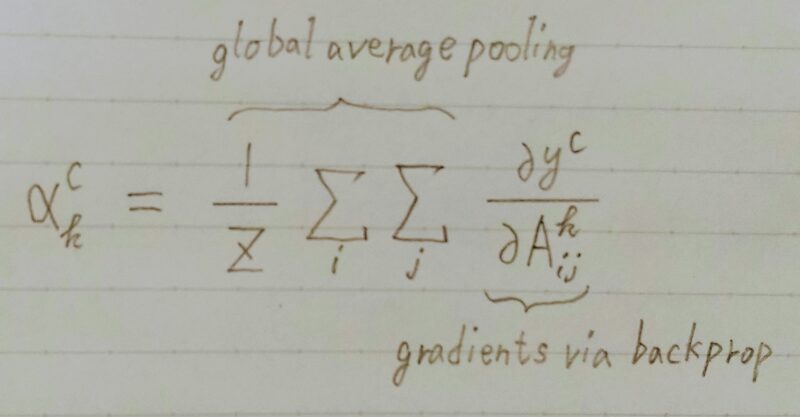
重みが大きいほど、特徴マップkがクラスcの予測にとって重要であると解釈できる
(batch_size,height,width,channel_size)
から(batch_size,channel_size)へ
特徴マップと線形結合するために
(batch_size,channel_size,1)と変形させる
【グローバル平均プーリング (Global Average Pooling,全体平均プーリング)】
引用元:「CVMLエキスパートガイド」
- k番目の特徴マップAkをαkc で加重平均をとり、ReLUの出力値をヒートマップとすると、ヒートマップは次式で表現できる。
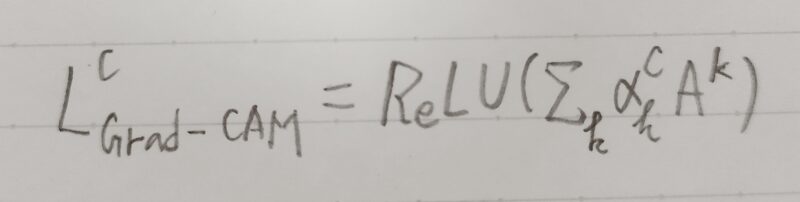
| Grad-CAM | CAM | |
|---|---|---|
| 特徴 | GAPがなくても可視化できる。 また、出力層が画像分類でなくてもよく、様々なタスクで使える。 | モデルのアーキテクチャにGAPがないと可視化できなかった |
Grad-CAMとは
引用元:R.R.Selvaraju,et al.,”Grad-cam:Visual explanation from deep networks via gradient-based localization”,2017
- explain メソッド
- クラス活性化ヒートマップ
- 誤分類の原因
4.LIME
- Local Interpretable Modelーagnostic Explanations
直訳)ローカルで解釈可能なモデル – 依存しない説明
原論文:”Why Should I Trust You?”:Explaining the Predictions of Any Classifier
https://arxiv.org/abs/1602.04938(KDD2016で採択) - 特定の入力データに対する予測について、その判断根拠を解釈・可視化するツール
ー表形式データ:「どの変数が予測に効いたのか」
ー画像データ:「画像のどの部分が予測に効いたのか」 - CNNやアンサンブルツリーなど様々な機械学習モデルに適用可能
- 単純で解釈しやすいモデルを用いて、複雑なモデルを近似することで解釈を行う
※「複雑なモデル」=「人間による解釈の困難なアルゴリズムを作った予測モデル」
例:決定木のアンサンブル学習器、ニューラルネットワークなど - LIMEへの入力は1つの個別の予測結果(モデル全体の近似は複雑すぎる)
- 対象サンプルの周辺のデータ空間からサンプリングして集めたデータセットを教師データとする。
データ空間の対象範囲内でのみ有効な近似用モデルを作成する。
下図はLIMEの原理を理解するための概念図である。
図において説明対象の「入力データ」を「赤色の太字の十字」とする。
原理は以下の手順である。
①入力データ(赤色の太字の十字)の周辺からサンプリングと予測を繰り返し行いデータセットを得る。
②得られたデータセットを教師データとする。
③教師データとして線形回帰モデルを作成する。
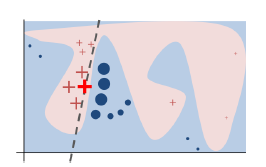
引用元:https://arxiv.org/abs/1602.04938
- 近似用モデル(線形回帰モデル)から予測に寄与した特徴量を選び解釈を行う ⇒ 難解なモデルを解釈したことと見なす。
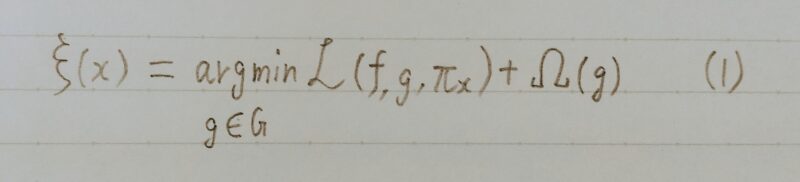
- G:線形回帰モデル、決定木などで、データを解釈するのに使われるモデル
- g:Gの中の解釈可能なモデルのうちいずれかを表す
- f:解釈したい結果を予測するモデル(解釈したいモデル)
- πx:fへの入力データxとどれだけあるデータが離れているかを表すあるデータとxとの類似度とも言える
- Ω(g):使っているモデルgがどれだけ複雑か、つまり解釈可能性のなさ、解釈のしずらさを表している
- ℒ(f,g,πx):πx が定義するxとの距離の指標を使ってgがfを近似する際、どれだけ不正解かを表す
つまり、解釈可能性と忠実性(gがfを近似する際の正確さ)の二つの質を保証するため、ℒ(f,g,πx)とΩ(g)の両方を小さく
- gへの入力にはxを加工したものを入れる(摂動を入れる)
- 画像であればスーパーピクセルという領域分割の技術を使いその一部をマスクしたり、テキストであれば単語をランダムに除去したり、表彰式データであればランダムに一部のデータを作り直したりしている。
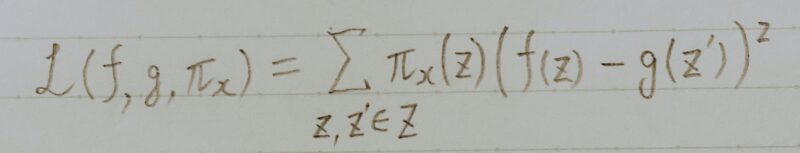
- z:説明したい例の近くのデータをサンプリングしたもの
- z´:zに摂動を入れたもの
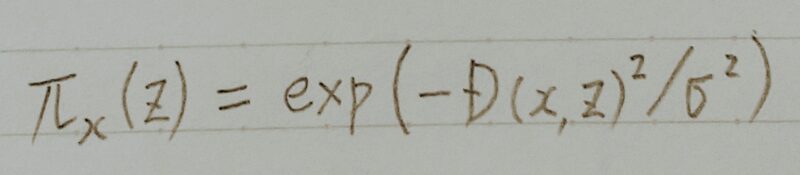
- 上式はxとzの距離関数(テキストであればコサイン類似度
画像の場合:ユークリッド距離など)にマイナスをかけたものをカーネル幅で割ったもの
- カーネル幅(σ):ハイパーパラメーターで、それを決める明確な方法がない。
- 解釈したいモデルにzを入れた結果と解釈可能なモデルにz´を入れた結果の差にzとxとの類似度で重み付けする
5.SHAP
- A Unified Approach to Interpreting Model Predictions
直訳)モデル予測を解釈するための統合アプローチ
論文:https://arxiv.org/pdf/1705.07874.pdf - 協力ゲーム理論の概念であるshapley value(シャープレイ値)を機械学習に応用した shapley valueが想定する状況:プレイヤーが協力し、それによって獲得した報酬を分配する ⇒これらの概念を機械学習に適用する
協力ゲーム理論:協力して得た報酬を、貢献度が異なるプレイヤーにどう分配するか
機械学習:モデルから出力された予測値を、貢献度が異なる特徴量にどう分配するか - CNNやアンサンブルツリーなど様々な機械学習モデルに適用可能
- Local Accuracy(局所的な精度):
ある入力をx、xの予測をf(x)とする。また、単純化した入力データをx’、x’に対する局所的近似をf'(x’)とする。このときf(x)とf'(x’)は同じになる。 - Missingness(欠落):
予測結果に影響を与えないような特徴量は、その予測に対して貢献していない。 - Consistency(一貫性):
fの方がf’よりもある特徴量xiが有るか無いかによって出力値に大きな変化があるならば、fの方がf’よりも貢献度が大きなる。
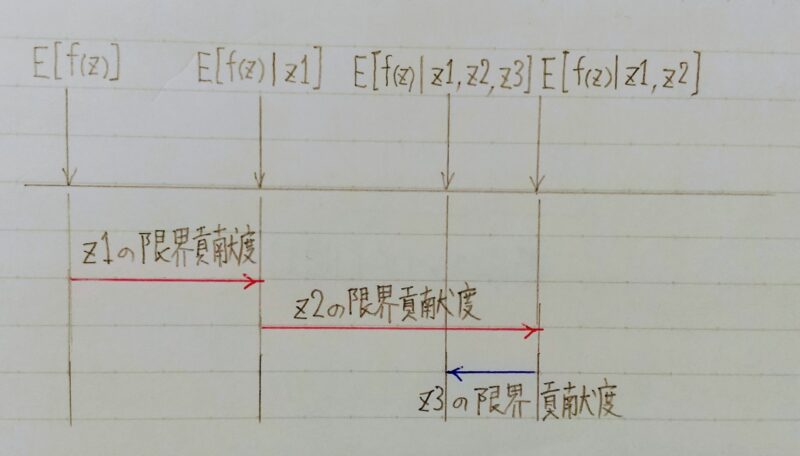
- z1、z2、z3:特徴量
- E[f(z)]:基本値であり、色々な決め方がある
- 代表的なものは着目したい特徴量を除いた、着目しない特徴量での予測を基本値とする方法
- これを全ての順序で計算し、平均をとったものがここでのshapley valueになる
Aさん、Bさん、Cさん が作業に参加する
一人で作業に参加した場合、
二人、三人で参加した場合の
報酬を表している
問題設定:
二人で参加した場合と
一人で参加した場合の
報酬の値を使って
三人で参加したときの
報酬の分配額を決める
貢献度が高い人に高い
報酬を分配したい
↓
どうすればいい?
「限界貢献度」
という概念を導入する
| 各作業 | 報酬 |
|---|---|
| Aさん | 4万円 |
| Bさん | 7万円 |
| Cさん | 5万円 |
| AさんとBさん | 10万円 |
| AさんとCさん | 16万円 |
| BさんとCさん | 20万円 |
| AさんととBさんとCさん | 35万円 |
BとCの作業に、Aが参加したときどれだけ報酬が増えるか
(AとBとC)ー(BとC)
の計算をAさんの限界貢献度とする
Cさんの限界貢献度のうちの一つは(BとC)ー(B)
Bさんの限界貢献度のうち一つはB
A,B,Cの順番で限界貢献度を計算していく時、
Aさんはそのまま4万円、Bさんは10万円ー4万円で6万円、
Cさんは35万円ー10万円で25万円となる。
これを全ての組み合わせで計算する。
Aの平均的な限界貢献度は
Aは(4+3+15+15+4+11)/6=8.7
Bは(6+7+7+15+19+19)/6=12.2
Cは(25+25+13+5+12+5)/6=14.2
| A | B | C | |
|---|---|---|---|
| A→B→C | 4万円 | 6万円 | 25万円 |
| B→A→C | 3万円 | 7万円 | 25万円 |
| B→C→A | 15万円 | 7万円 | 13万円 |
| C→B→A | 15万円 | 15万円 | 5万円 |
| A→C→B | 4万円 | 19万円 | 12万円 |
| C→A→B | 11万円 | 19万円 | 5万円 |
| 協力ゲーム理論 | 機械学習 | |
|---|---|---|
| 考え方 | 協力して得た報酬を、貢献度が異なるプレイヤーにどう分配するか | モデルから出力された予測値を、貢献度が異なる特徴量にどう分配するか |
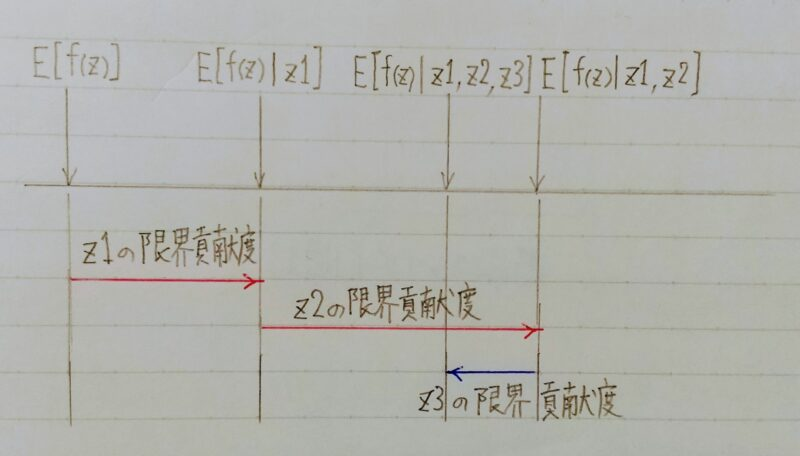
- 特徴量z1のみを使って予測した値と基本値との差でz1の限界貢献度が分かる
- 特徴量z1、z2を使って予測した値と特徴量z1のみを使って予測した値との差で
z2の限界貢献度が分かる - z1、z2、z3を使って予測した値と特徴量z1、z2を使って予測した値との差で
z3の限界貢献度が分かる - これを全ての順序で計算し、平均をとったものがここでのshapley valueになる。
6.まとめ
最後まで読んで頂きありがとうございます。
皆様のキャリアアップを応援しています!!

コメント