- 「非線形回帰モデル」について学びたいけど理解できるか不安・・・
- 「非線形回帰モデル」についてどこから学んでいいか分からない?
- 「非線形回帰モデル」を体系的に教えて!
「人工知能(AI:Artificial intelligence)」を勉強する際、その基礎である「機械学習」の考え方を理解していないため人工知能が理解できないケースは非常に多いです。
私は過去に基本情報技術者試験(旧:第二種情報処理技術者試験)に合格し、また2年程前に「一般社団法人 日本ディープラーニング協会」が主催の「G検定試験」に合格しました。現在、「E資格」にチャレンジ中ですが3回不合格になり、この経験から学習の要点について学ぶ機会がありました。
そこでこの記事では、「機械学習」のうち「非線形回帰モデル」についてポイントを解説します。
この記事を参考にして「非線形回帰モデル」が理解できれば、E資格に合格できるはずです。
目次
1.アウトライン
- 複雑な非線形構造を内在する現象に対して、非線形回帰モデリングを実施
〇データの構造を線形で捉えられる場合は限られる
〇非線形な構造を捉えられる仕組みが必要 - パラメータの推定問題:最小2乗法・尤度最大化
2.数学的定式化
2.1 非線形回帰モデルの説明
- 基底展開法
〇回帰関数として、基底関数(既知の非線形関数)とパラメータベクトルの線形結合を使用
〇未知のパラメータは線形回帰モデルと同様に最小2乗法や最尤法により推定
yi = f(xi) + εi yi = w0 + Σ wjφj(xi) + εi - よく使われる基底関数
〇多項式関数
〇ガウス型基底関数
〇スプライン関数/Bスプライン関数 - 1次元の基底関数に基づく非線形回帰
多項式(1~9次) φj = xj
ガウス型基底 φj(x) = exp{(x – μj)2/2hj} - 2次元の基底関数に基づく非線形回帰
2次元ガウス型基底関数 φj(x) = exp{(x – μj)T(x – μj)/2hj}
説明変数
非線形関数ベクトル
非線形関数の計画行列
最尤法による予測値
基底展開法も線形回帰と同じ枠組みで推定可能 - 未学習(underfitting)と過学習(overfitting)
〇学習データに対して、十分小さな誤差が得られないモデル→未学習
■(対策)モデルの表現力が低いため、表現力の高いモデルを利用する
〇小さな誤差は得られたけど、テスト集合誤差との差が大きいモデル→過学習
■(対策1)学習データの数を増やす
■(対策2)不要な基底関数(変数)を削除して表現力を抑止←モデルの複雑さ
■(対策3)正則化法を利用して表現力を抑止←調整する2つの方法 - 不要な基底関数を削除
〇基底関数の数、位置やバンド幅によりモデルの複雑さが変化
〇解きたい問題に対して多くの基底関数を用意してしまうと過学習の問題がおこるため、適切な基底関数を用意(CVなどで選択)
- 正則化法(罰則化法)
〇「モデルの複雑さに伴って、その値が大きくなる正則化項(罰則項)を課した関数」を最小化
〇正則化項(罰則項)
■形状によっていくつもの種類があり、それぞれ推定量の性質が異なる
〇正則化(平滑化)パラメータ
■モデルの曲線の滑らかさを調節→適切に決める必要あり

- 基底関数の数(k)が増加するとパラメータが増加し、残差は減少(モデルが複雑化)
- 正則化項(罰則項)の役割
〇無い→最小2乗推定量
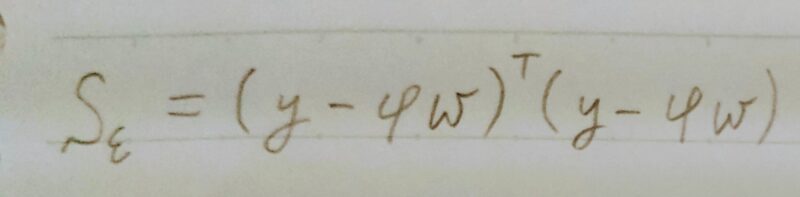
〇L1ノルムを利用→Lasso推定量
→ スパース推定 いくつかのパラメータを正確に0に推定
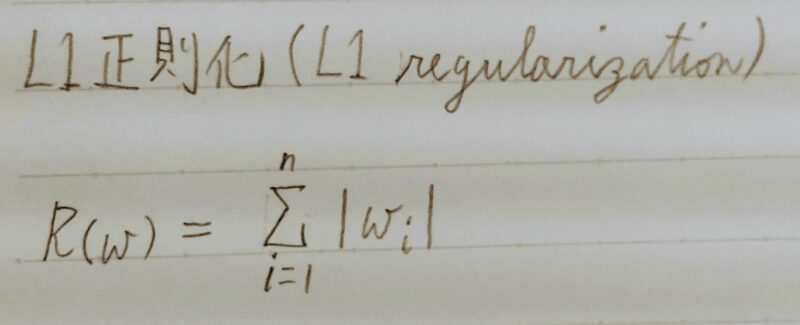
〇L2ノルムを利用→Ridge推定量
→ 縮小推定 パラメータを0に近づけるよう推定
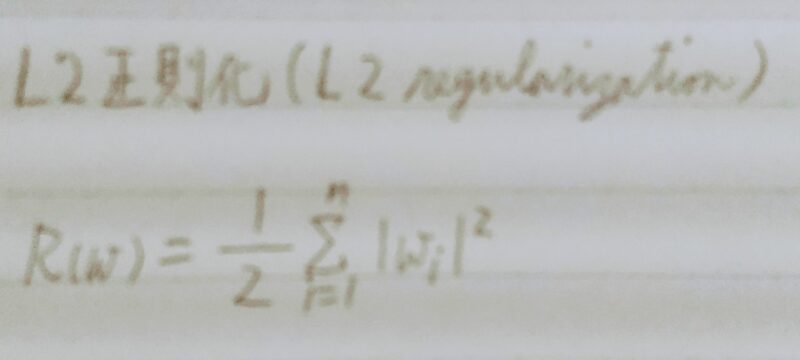
- 正則化パラメータの役割
〇小さく→制約面が大きく
〇大きく→制約面が小さく - 適切なモデル(汎化性能が高いモデル)は交差検証法で決定
- 汎化性能
〇学習に使用した入力だけではなく、これまで見たことのない新たな入力に対する予測性能
■ (学習モデルではなく)汎化誤差(テスト誤差)が小さいものがよい性能を持ったモデル。学習に使ったデータと同じデータで検証(モデルの学習データへの当てはまりの良さ)
学習誤差
検証誤差
- 手元のモデルがデータに未学習しているか過学習しているか
〇訓練誤差もテスト誤差もどちらも小さい→汎化しているモデルの可能性
〇訓練誤差は小さいがテスト誤差が大きい→過学習
〇訓練誤差もテスト誤差もどちらも小さくならない→未学習
〇回帰の場合には陽に解が求まります(学習誤差と訓練誤差の値を比較) - ホールドアウト法
〇有限のデータを学習用とテスト用の2つに分割し、「予測精度」や「誤り率」を推定する為に使用
■学習用を多くすればテスト用が減り学習精度は良くなるが、性能評価の精度は悪くなる。
■逆にテスト用を多くすれば学習用が減少するので、学習そのものの精度が悪くなることになる。
■手元にデータが大量にある場合を除いて、良い性能評価を与えないという欠点がある。
■大規模データに対しては確率的勾配降下法の方が計算コストが小さい。
■ホールドアウト法と交差検証の使い分け
一般的には、一回の訓練が数時間以内で終わるものであれば、交差検証を利用し、検証を素早く行いたい場合などは、ホールドアウト法を使う。
〇基底展開法に基づく非線形回帰モデルでは、基底関数の数、位置、バンド幅の値とチューニングパラメータのホールドアウト値を小さくするモデルで決定する。
2.2 パラメータの推定
編集中
2.3 バイアス・バリアンスのトレードオフ
「バイアス」と「バリアンス」の関係
- バイアス(Bias):
予測値と正解値とのズレ(=偏り誤差)を指す。(=シミュレーション(訓練データ)に対するモデルの誤差)
この予測誤差は、モデルの仮定に誤りがあることから生じる。モデルによる予測においてバイアス(偏り誤差)が大きすぎる場合、そのモデルは入力と出力の関係性を正確に表現できていない。いわゆる学習不足の状態。モデルの複雑性(表現力)が大きくなると過学習になりやすくバイアスは小さくなる。 - バリアンス(Variance):
予測値の広がり(=ばらつき誤差)を指す。(=実際(テストデータ)に対するモデルの誤差)
この予測誤差は、訓練データの揺らぎから生じる。バリアンス(ばらつき誤差)が大きすぎる場合、そのモデルは訓練データのノイズまで学習してしまっている。いわゆる過学習の状態。モデルの複雑性(表現力)が大きくなると過学習になりやくバリアンスは大きくなる。 - バイアスとバリアンスはトレードオフの関係
| 学習不足 | 過学習 | |
|---|---|---|
| バイアス(Bias) | 大 | 小 |
| バリアンス(Variance) | 小 | 大 |
2.4 モデルの評価(交差検証)
- データを学習用と評価用に分割(5分割の例)
- 検証データで各モデルの精度を計測
- 精度の平均をCV値と呼ぶ(モデル1の汎化性能)
チューニングパラメータは固定 - グリッドサーチ
〇全てのチューニングパラメータの組み合わせで評価値を算出
〇最も良い評価値を持つチューニングパラメータを持つ組み合わせを「いいモデルのパラメータ」として採用
3.まとめ
最後まで読んで頂きありがとうございます。
皆様のキャリアアップを応援しています!!

コメント