- 機械学習に興味はあるけど「統計学」を理解できるか不安・・・
- 「統計学」についてどこから学んでいいか分からない?
- 「統計学」を分かりやすく教えて!
「統計学」は人工知能(AI)を含む機械学習において用いられれている重要な数学ですが、興味があっても難しそうで何から学んだらよいか分からず、勉強のやる気を失うケースは非常に多いです。
私は過去に基本情報技術者試験(旧:第二種情報処理技術者試験)に合格し、また2年程前に「一般社団法人 日本ディープラーニング協会」が主催の「G検定試験」に合格しました。現在、「E資格」にチャレンジ中ですが3回不合格になり、この経験から学習の要点について学ぶ機会がありました。
そこでこの記事では、「統計学」のうち「条件付き確率」や「ベイズの定理」等についてポイントを解説します。
この記事を参考にして「条件付き確率」や「ベイズの定理」等が理解できれば、E資格に合格できるはずです。
<<「条件付き確率」や「ベイズの定理」等のポイントを今すぐ見たい方はこちら
1.統計
機械学習において大量のデータを適切に扱う必要が!
↓
- 大量のデータから特徴を見つけ出し、分析するための手法
- 統計学は独自の専門用語に加え、数学の言葉で記述されている。

統計学の専門用語や数式これらを「読める」ようになりたい!

統計学の世界を冒険するための基礎を身に着けよう!
ここでは、データの定量化に役立つ情報科学の考え方を紹介
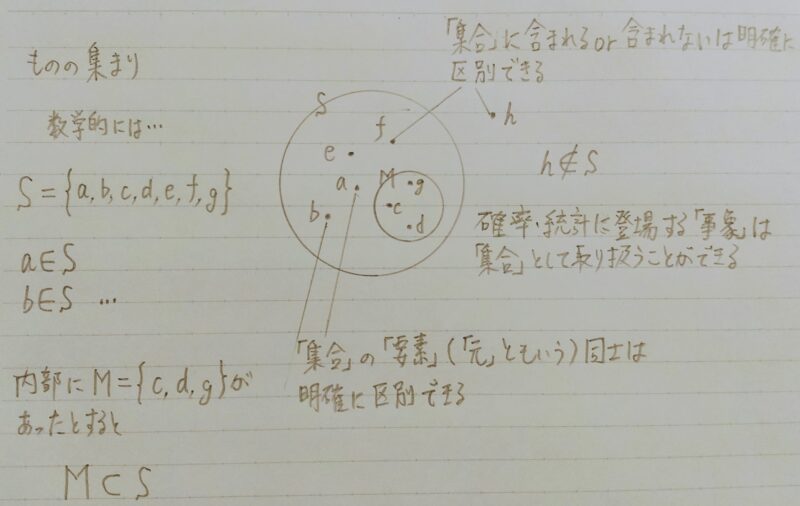
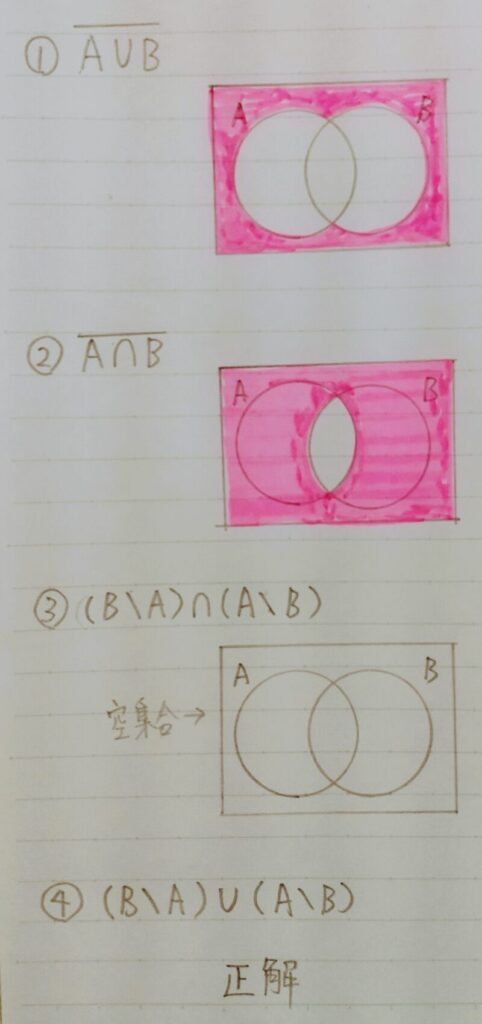
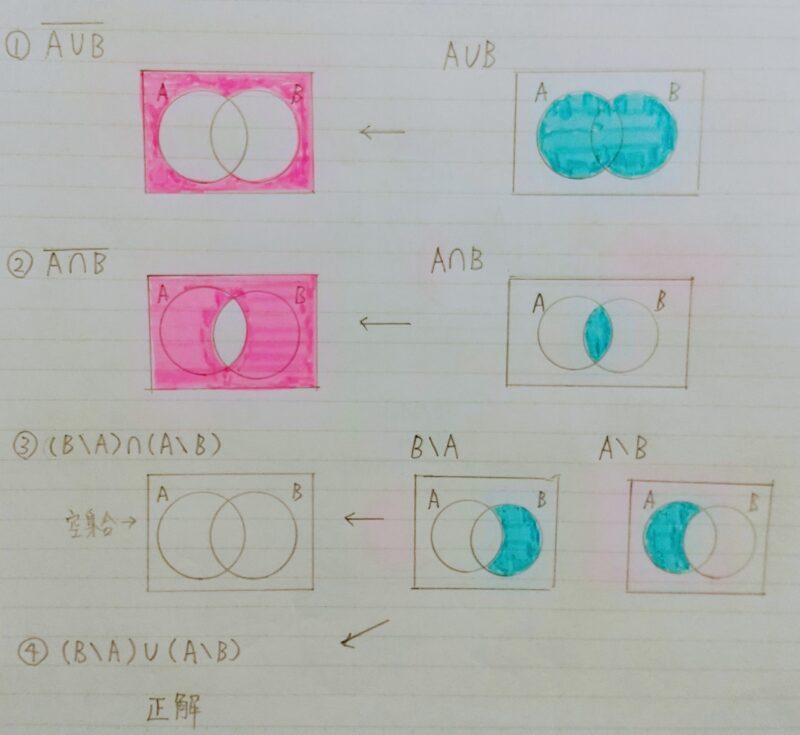
1.1 集合とは何か?
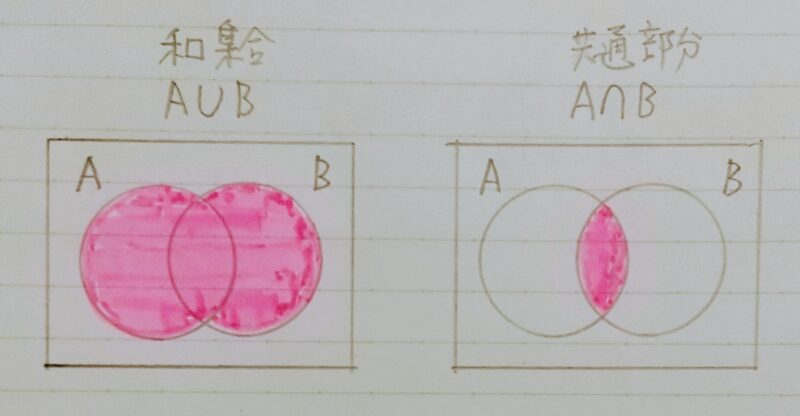
1.2 和集合と共通部分
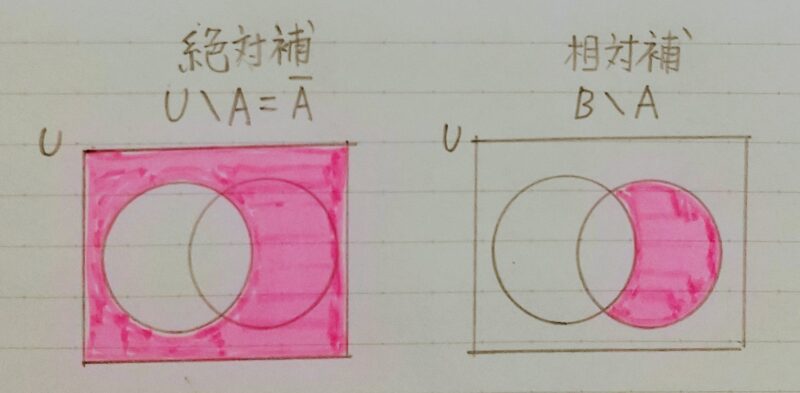
1.3 絶対補と相対補
1.4 例題
〈問題〉
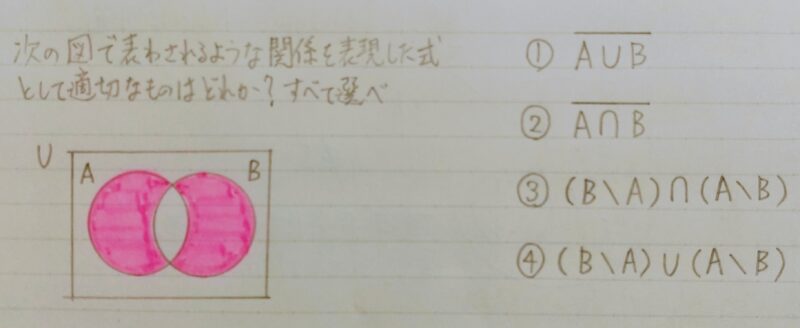
〈解答〉
[affi id=3]
[affi id=6]
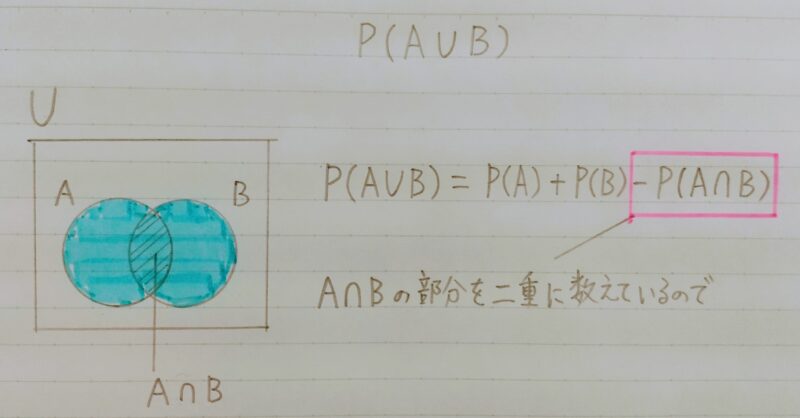
2.確率
| 頻度確率(客観確率) | ベイズ確率(主観確率) | |
| 内 容 | 発生する頻度 | 信念の度合い |
| 具体例 | 「10本のうち1本だけ当たりクジを引いて当選する確率を調べたところ10%であった」という事実 | 「あなたは40%の確率でインフルエンザです」という診断 |
2.1 確率の定義

- Q. オッズ(odds)を表した式を下記の選択肢から選べ。
オッズ(odds)とは確率pで起こる事象Aについて、Aが起こる確率と起こらない確率の比であり、競馬などでも使われている。
1. 1/p
2. p/(1-p)
3. 1/(1+p)
4. (1-p)/p - A. 正解は2.p/(1-p)
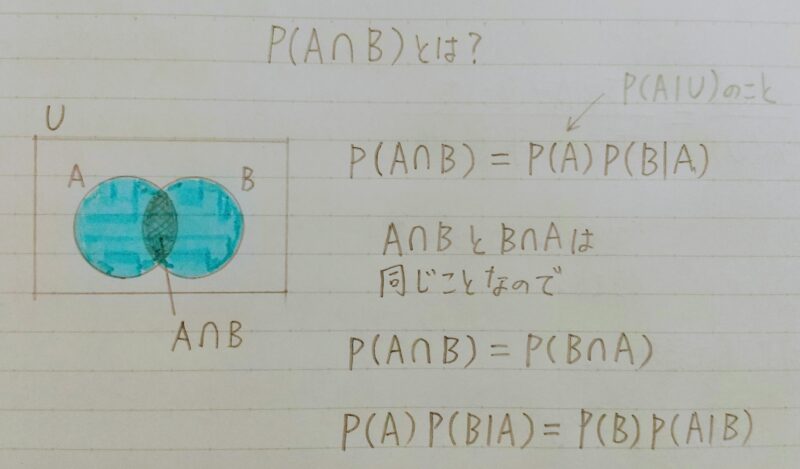
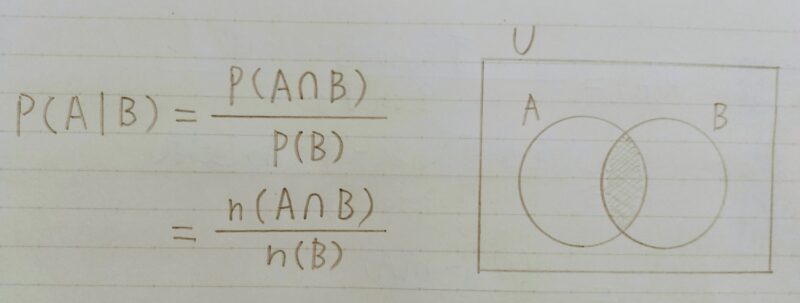
2.2 条件付き確率
- ある事象Bが与えられた下で、Aとなる確率
・例:雨が降っている条件下で交通事故に遭う確率
2.3 独立な事象の同時確率
- お互いの発生には因果関係のない事象Aと事象Bが同時に発生する確率
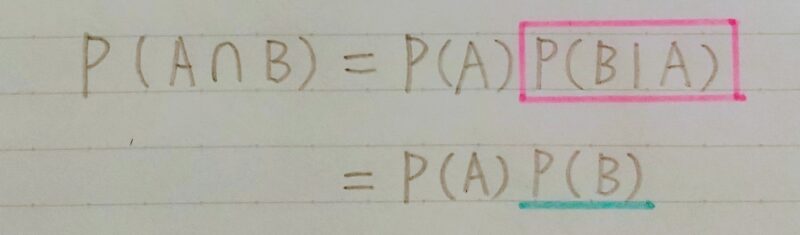
2.4 ベイズの定理
- 一般的に事象Aと事象Bに対して・・・
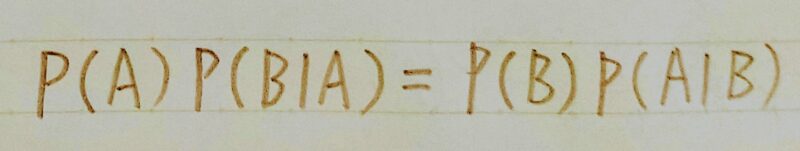
↓
実データの観測を通してモデルパラメータBのより確からしい確率分布を推定
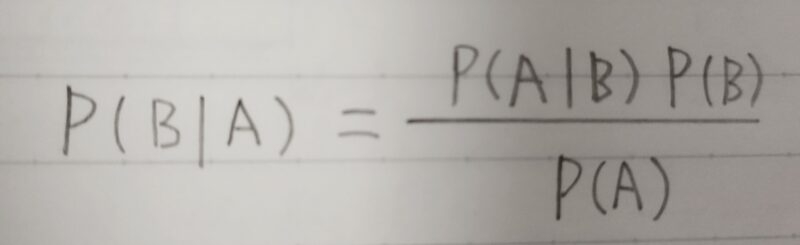
- P(B|A)とP(B)の関係
- P(B)(=事前分布)を一様分布とした場合、
最尤法によるBの推定値 = P(B|A)(=事後確率)を最大にするB
- P(B)(=事前分布)を一様分布とした場合、
- P(A)の導出
- ベイズ則の式②において、P(A)は一般的に下式により導出できる。
- ベイズ則の式②において、P(A)は一般的に下式により導出できる。
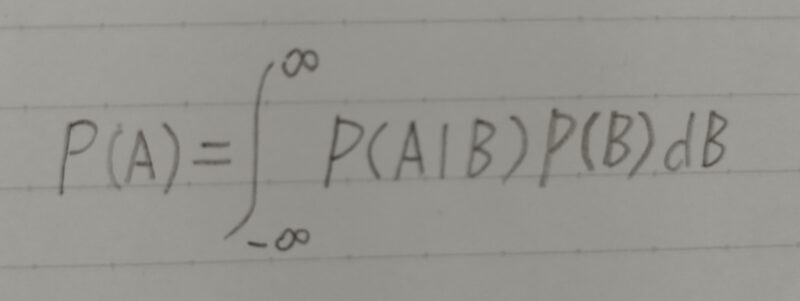
パラメータBが多くなると、積分計算が不可能
↓
P(B|A)(事後確率分布)を解析的に導くことができない。
↓
近似推論(積分回避)
↓
マルコフ連鎖モンテカルロ法
(サンプリングアルゴリズム)
マルコフ連鎖モンテカルロ法とは・・・
引用元:「HEADBOOST」
ベイズ推定において、事後分布を求めるのが計算上余りにも困難な場合に、事前分布と尤度分布を材料として乱数を無作為抽出することで、事後分布を概算する方法のことです。
2.5 例題
- Q1.ある街の子供たちは毎日1/4の確率で飴玉をもらうことができ、飴玉をもらうと1/2の確率で笑顔になるという。その街の笑顔な子供が飴玉をもらっている確率を求めよ。(ただし、この街の子供たちが笑顔でいる確率は1/3である。)
- A1.例題の内容を整理すると
P(飴玉):飴玉をもらう確率=1/4
P(笑顔):笑顔でいる確率=1/3
P(笑顔|飴玉):飴玉が与えられた下で、笑顔となる確率=1/2
P(飴玉|笑顔):笑顔でいる下で、飴玉をもらっている確率=?
P(飴玉) × P(笑顔|飴玉) = P(笑顔∧飴玉)
1/4 × 1/2 = 1/8
P(笑顔∧飴玉) = P(飴玉∧笑顔) ← ベイズの定理
↑
( P(飴玉)×P(笑顔|飴玉)=P(笑顔)×P(飴玉|笑顔))
P(飴玉∧笑顔) = P(笑顔) × P(飴玉|笑顔)
1/8 = 1/3 × P(飴玉|笑顔)
P(飴玉|笑顔) = 1/8/(1/3)
したがって答えは
P(飴玉|笑顔)=3/8
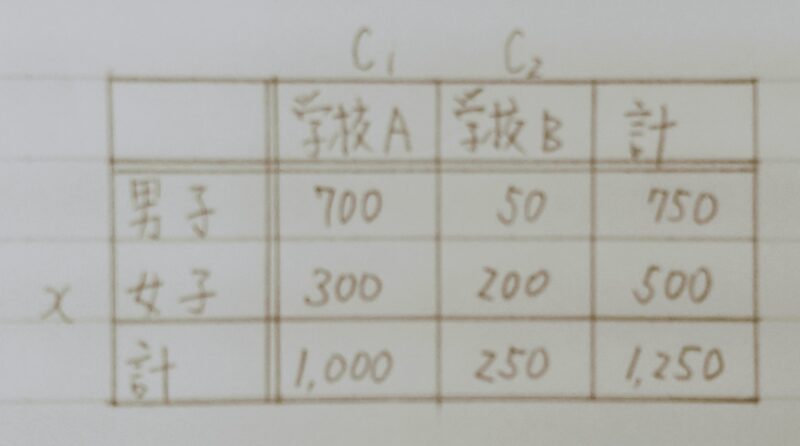
- Q2.ある学生の性別データから学校Aか学校Bかを判別するモデルを考える。学校Aの男女比は7:3で生徒数は1000人,学校Bの男女比は2:8で生徒数は250人であるとする。ある入力データxiについて性別が女子であった時、学校Aに属する確率を求めよ。ただし、ここで性別は男子もしくは女子しか考えないものとする。
- A2.

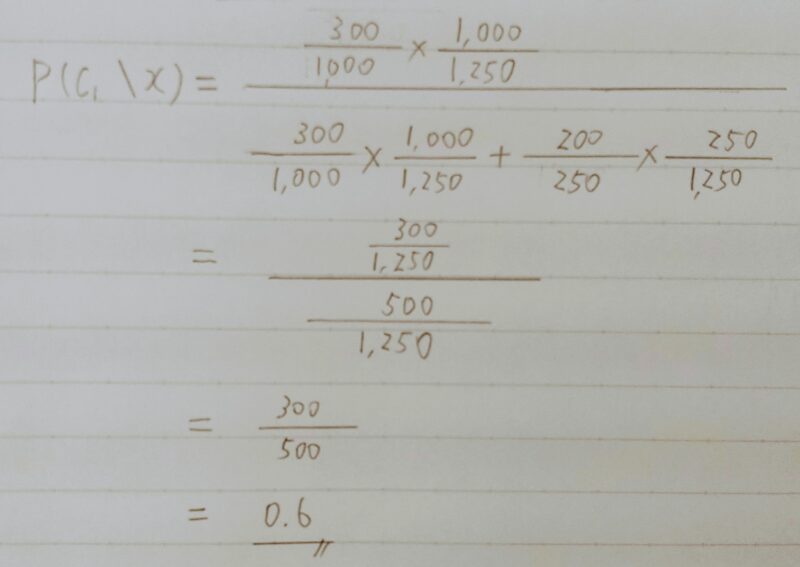
- Q3.罹患(りかん)率0.01%の病気の罹患状況について考える。この病気の検査方法では、実際に罹患している人間が陽性と診断される確率が98%、罹患していない人が陰性と診断される確率は80%となる。
この時、陽性だと診断された場合、本当に罹患している確率として最も近い選択枝を以下の中から選びなさい。
なお、陽性だと診断される確率は20%とする。
補足)「罹患」とは病気にかかること、疾病すること。 - A3.
x:罹患
C:陽性
とすると、今回求めたい「陽性だと診断された場合、本当に罹患している確率」は次のように表現できる。
P(x|C):陽性だと診断された場合、本当に罹患している確率
上記をベイズの定理を用いて表現すると、
P(x|C)=P(C|x)・P(x)/P(C)・・・①
ここで、
P(C|x)=98%
P(x)=0.01%
P(C)=20%
であるから、これらの値を式①に代入すると
P(x|C)=98・0.01/20
=0.049
≒0.05%
3.まとめ

最後まで読んで頂きありがとうございます。
皆様のキャリアアップを応援しています!!

コメント