- 機械学習には興味があるけど「統計学」を理解できるか不安・・・
- 「統計学」についてどこから学んでいいか分からない?
- 「統計学」を体系的に教えて!
「統計学」はAI(人工知能)を含む機械学習において用いられれている重要なものですが、興味があっても難しそうで何から学んだらよいか分からず、勉強のやる気を失うケースは非常に多いです。
私は過去に基本情報技術者試験(旧:第二種情報処理技術者試験)に合格し、また2年程前に「一般社団法人 日本ディープラーニング協会」が主催の「G検定試験」に合格しました。現在、「E資格」にチャレンジ中ですが3回不合格になり、この経験から学習の要点について学ぶ機会がありました。
そこでこの記事では、「統計学」のうち「期待値」や「標準偏差」等について学習する際のポイントについて解説します。
この記事を参考にして「統計学」が理解できれば、E資格に合格できるはずです。
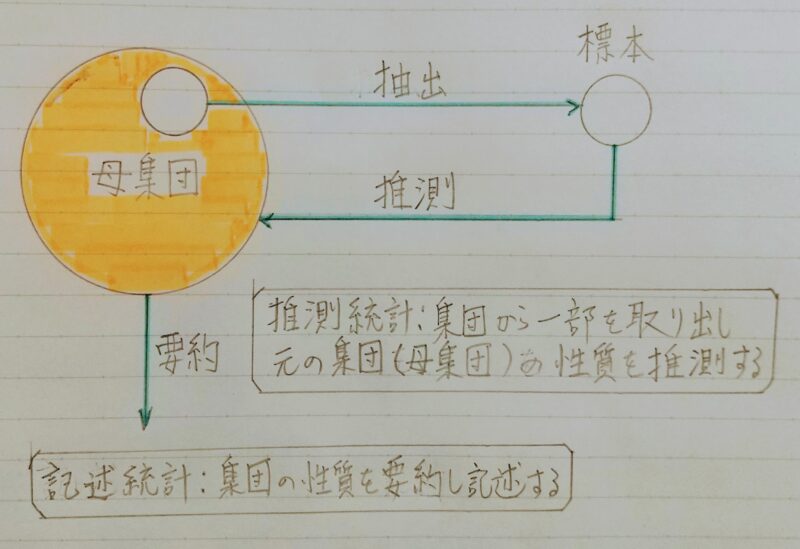
1.記述統計と推測統計
1.1 確率変数と確率分布
- 事象と結び付けられた数値
- 事象そのものを指すと解釈する場合も多い
- 事象の発生する確率の分布
- 離散値であれば表に示せる
| 事象 | 裏が0枚, 表が4枚 | 裏が1枚, 表が3枚 | 裏が2枚, 表が2枚 | 裏が3枚, 表が1枚 | 裏が4枚, 表が0枚 |
|---|---|---|---|---|---|
| 確率変数(裏を0, 表を1と対応させ 和をとった) | 4 | 3 | 2 | 1 | 0 |
| 事象が発生した 回数 | 75 | 300 | 450 | 300 | 75 |
| 事象と対応する 確率 | 1/16 | 4/16 | 6/16 | 4/16 | 1/16 |
1.2 期待値
- その分布における、確率変数の・・・
平均の値 or 「ありえそう」な値
| 事象X | X1 | X2 | ・・・ | Xn |
|---|---|---|---|---|
| 確率変数f(X) | f(X1) | f(X2) | ・・・ | f(Xn) |
| 確率P(X) | P(X1) | P(X2) | ・・・ | P(Xn) |
- 連続する値なら・・・
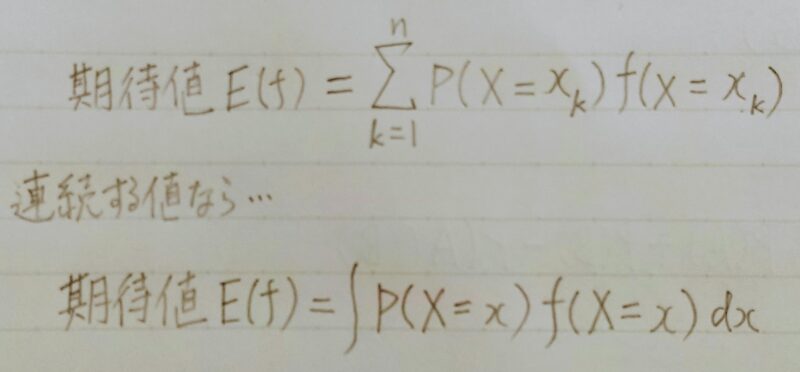
1.3 分散と共分散
分散
- データの散らばり具合
- データの各々の値が期待値からどれだけズレているのか平均したもの
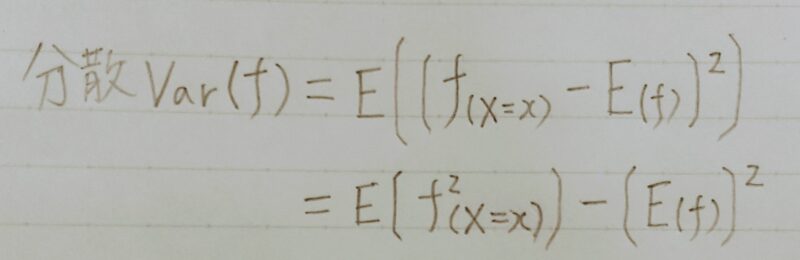
共分散
- 2つのデータ系列の傾向の違い
- 正の値を取れば似た傾向
- 負の値をとれば逆の傾向
- ゼロを取れば関係性に乏しい
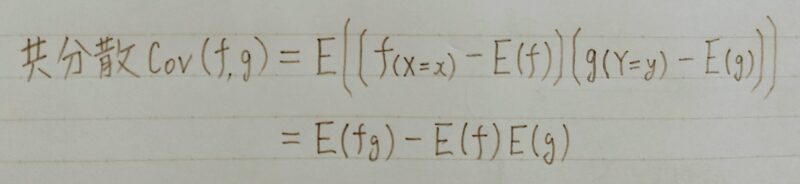
1.4 分散と標準偏差
分散は2乗してしまっているので元のデータと単位が違う。
↓
2乗することの逆演算(=平方根を求める)をすれば元の単位に戻る。
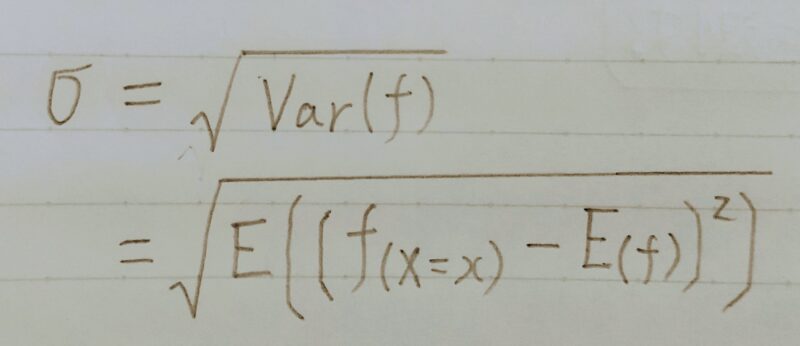
2.確率分布
2.1 様々な確率分布
ベルヌーイ分布
- コイントスのイメージ
- 裏と表が出る割合が等しくなくとも扱える
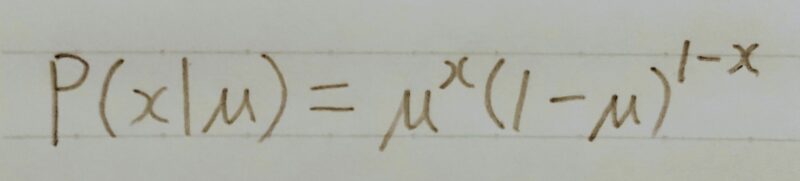

マルチヌーイ(カテゴリカル)分布
- サイコロを転がすイメージ
- 各面の出る割合が等しくなくとも扱える

二項分布
- ベルヌーイ分布の多試行版
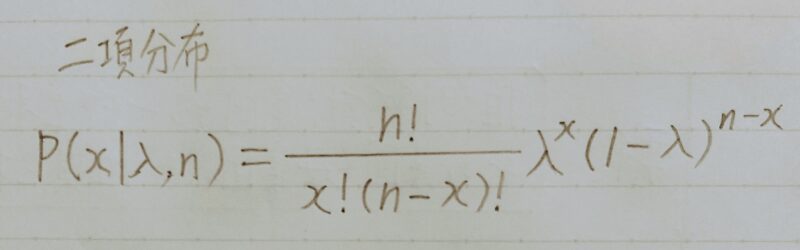
ガウス分布(1次元正規分布)
- 釣鐘型の連続分布
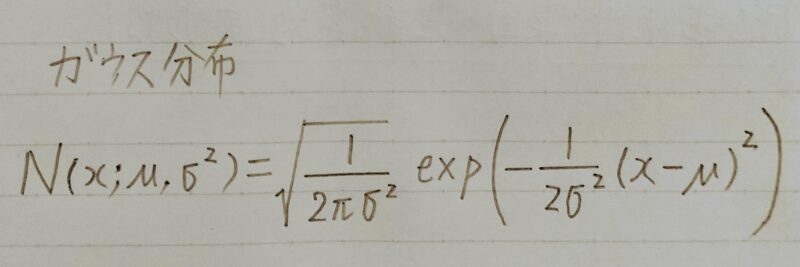
μ:平均
σ:標準偏差
(σ2:分散)

ガウス分布は真の分布が分からなくてもサンプルが多ければ正規分布に近づくよ!
Q.ベルヌーイ分布は離散確率分布の一種であり、例えば、確率変数Xが0.2の確率で1をとり、0.8の確率で0をとるような分布である。この試行を10回行った時の確率分布の平均と分散を求めよ。
A.平均は0.2×10回=2
分散は0.2×0.8×10回=1.6
2.2 連続型確率分布
2.2.1 確率
連続型確率変数の場合の確率は、次の式によって計算できる。
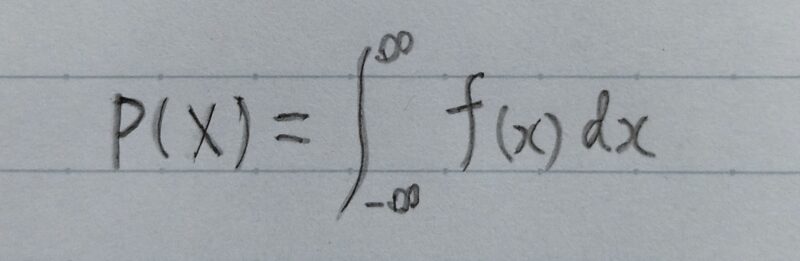
2.2.2 期待値
連続型確率変数の場合の期待値は、次の式によって計算できる。
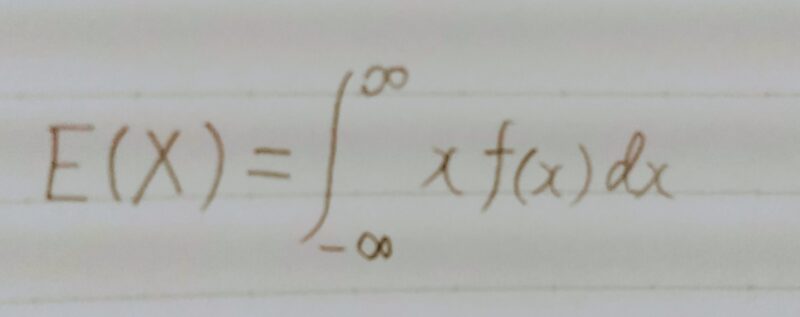
計算式
次の連続型確率変数Xを表す確率密度関数f(x)に対する期待値E(X)を求めよ。
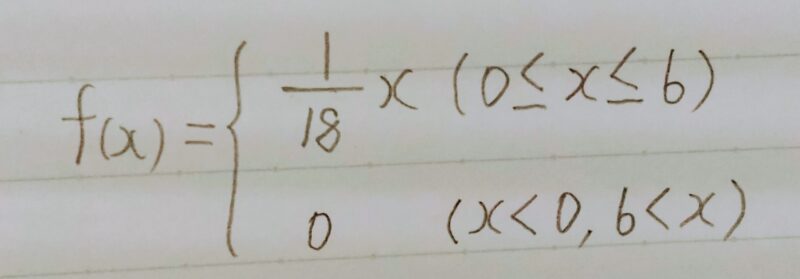
【解答】
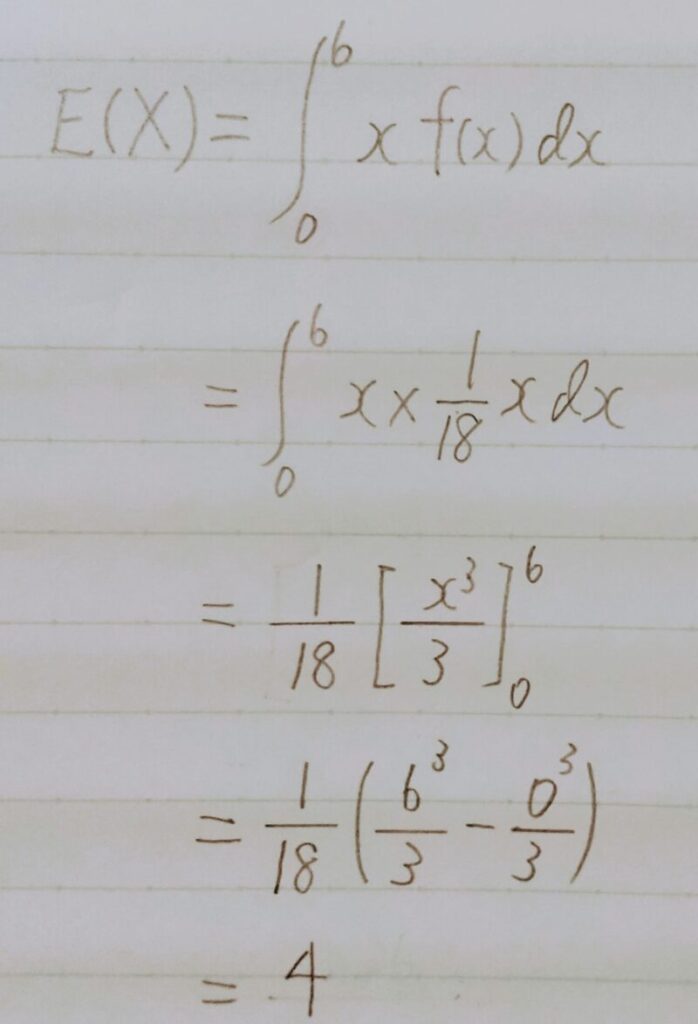
期待値の計算例
2.2.3 確率密度関数になる重要な条件
- 確率密度関数f(x)の値は常に0以上
- 「取り得る値の全範囲」にわたって、確率密度関数f(x)を積分すると1になる。つまりp(全範囲)=1となる。
- 連続型確率変数の分散と期待値の関係式
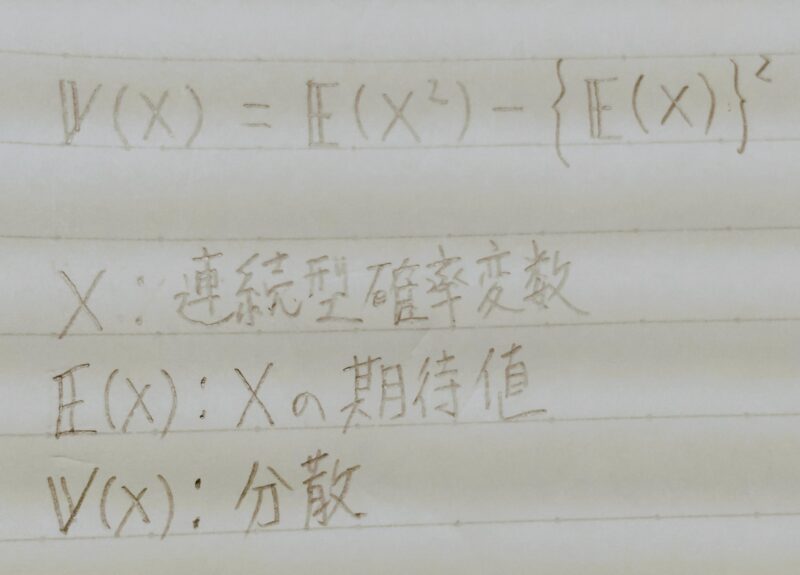
3.推定
母集団を特徴づける母数(パラメーター:平均など)を統計学的に推測すること。

推測統計:集団から一部を取り出し元の集団(母集団)の性質を推測する
点推定:
平均値などを1つの値に推定すること。
区間推定:
平均値などが存在する範囲(区間)を推定すること
3.1 推定量と推定値
推定量(estimator):
パラメータを推定するために利用する数値の計算方法や計算式のこと。推定関数とも。
推定値(estimate):
実際に試行を行った結果から計算した値


推定量と推定値は日本語ではあまり区別しないことも・・・
3.2 標本平均
母集団から取り出した標本の平均値
サンプル数が大きくなれば、母集団の値に近づく
→ 一致性
サンプル数がいくらであっても、その期待値は母集団の値と同様
→ 不偏性
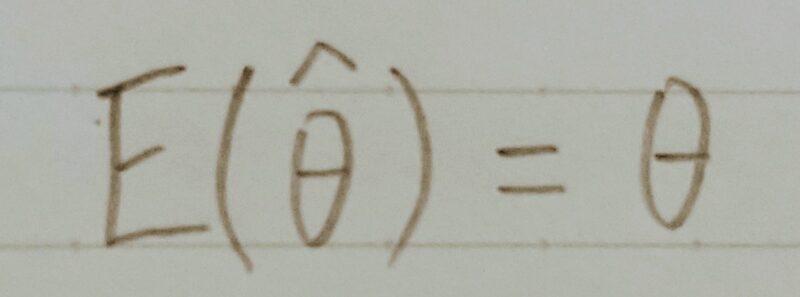
3.3 標本分散
サンプルサイズをnとすると・・・
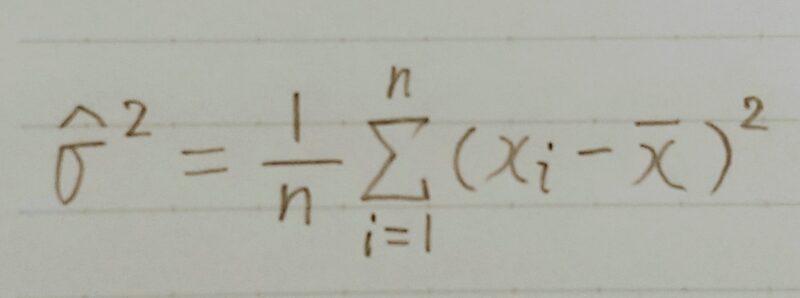
一致性は満たすが・・・
不偏性は満たさない!!
思考実験:
たくさんのデータのばらつき具合
少数のデータのばらつき具合

どちらがよりばらつくかな?
3.4 不偏分散
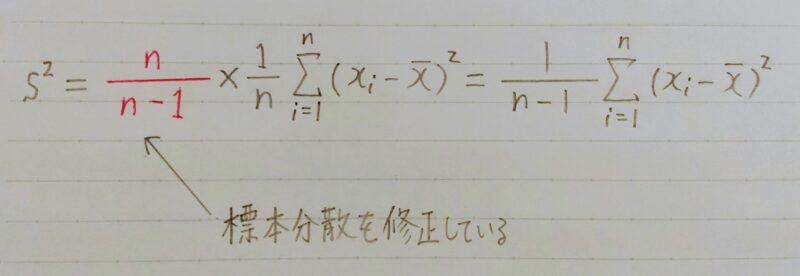

なぜこのような数をかけるのなか?
4.まとめ
最後まで読んで頂きありがとうございます。
皆様のキャリアアップを応援しています!!

コメント