- 深層学習モデルの「性能向上の方法」を理解しているか不安・・・
- 深層学習モデルの「性能向上の方法」がよく分からない?
- 深層学習モデルの「性能向上の方法」を分かりやすく教えて!
深層学習モデルの「性能向上の方法」には、勾配消失問題の対策、学習率の最適化、過学習抑制対策など様々なものがありますが、難しそうで何から学んだらよいか分からず、勉強のやる気を失うケースは非常に多いです。
私は過去に基本情報技術者試験(旧:第二種情報処理技術者試験)に合格し、また2年程前に「一般社団法人 日本ディープラーニング協会」が主催の「G検定試験」に合格しました。現在、「E資格」にチャレンジ中ですが3回不合格になり、この経験から学習の要点について学ぶ機会がありました。
そこでこの記事では、深層学習モデルの「性能向上の方法」についてポイントを解説します。
この記事を参考にして深層モデルの「性能向上の方法」が理解できれば、E資格に合格できるはずです。
<<深層モデルの「性能向上の方法」のポイントについて今すぐ見たい方はこちら
勾配消失問題の解決法
誤差逆伝播法が下位層に進んでいく連れて、勾配がどんどん緩やかになっていく。そのため、勾配降下法による更新では下位層のパラメータはほとんど変わらず、訓練は最適値に収束しなくなる。
y:予測値
d:目標値
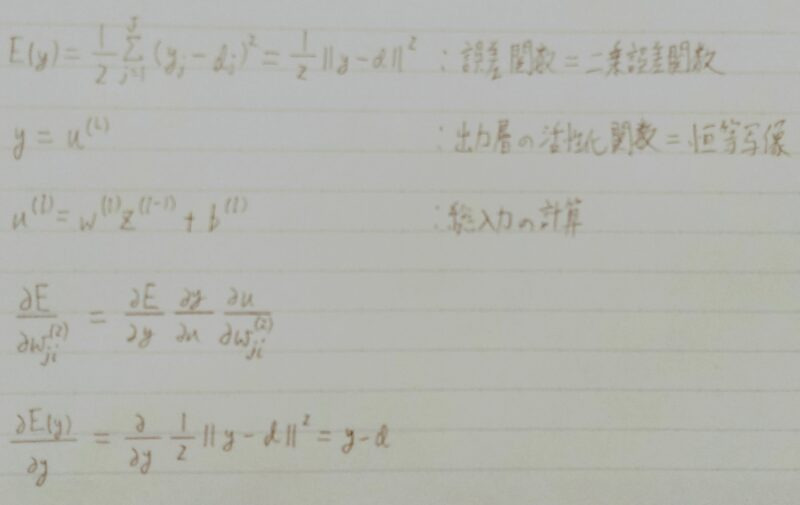

サンプルコード
def sigmoid(x):return 1/(1+np.exp(x))
数式
f(u) = 1/(1+e-u)
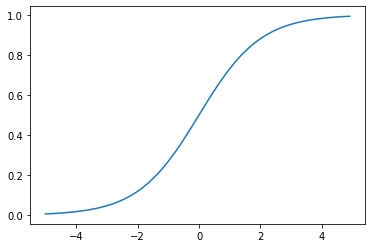
0~1の間に緩やかに変化する関数で、ステップ関数ではON/OFFしかない状態に対し、信号の強弱を伝えられるようになり、予想ニューラルネットワーク普及のきっかけとなった。
大きな値では出力の変化が微小なため、勾配消失問題を引き起こすことがあった。
Q.シグモイド関数を微分した時、入力値が0の時に最大値をとる。その値とは?
A.0.25

- 活性化関数の選択
- 重みの初期値設定
- Batch正規化
活性化関数の選択
- 現在、最も使われている活性化関数
- シグモイド関数の勾配消失問題を解消
- 勾配消失問題の回避とスパース化に貢献することで良い成果をもたらしている。
サンプルコード
def relu(x):
return
np.maximum(0,x)
数式
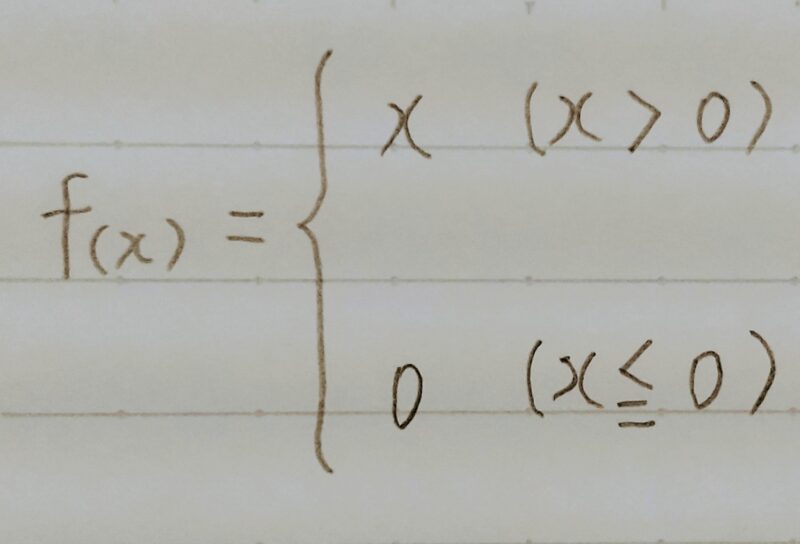
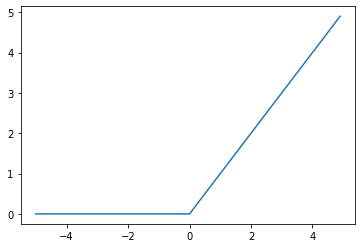
重みの初期値設定ーXavier
- ReLU関数
- シグモイド(ロジスティック)関数の場合
- 双曲線正接関数の場合
network[‘W1’] = np.random.randn(input_layer_size, hidden_layer_size) / np.sqrt(input_layer_size)
network[‘W2’] = np.random.randn(hidden_layer_size, output_layer_size) / np.sqrt(hidden_layer_size)
↓
■重みの要素を、前の層のノード数の平方根で除算した値
- ReLU関数の場合
- シグモイド(ロジスティック)関数の場合
- 双曲線正接関数の場合
■重みの要素を、前の層のノード数の平方根で除算した値に対し√2をかけ合わせた値
Batch Normalization(バッチ正規化)
- ミニバッチ単位で、入力値のデータの偏りを抑制する手法
- 「Batch Normalization」はどこに使う?
⇒ 活性化関数に値を渡す前後に、「Batch Normalization」の処理を学んだ層を加える。
※Batch Normalizationは学習時のみ使用し、検証時、テスト時は使用しない。
↓
Batch Normalization への入力値は
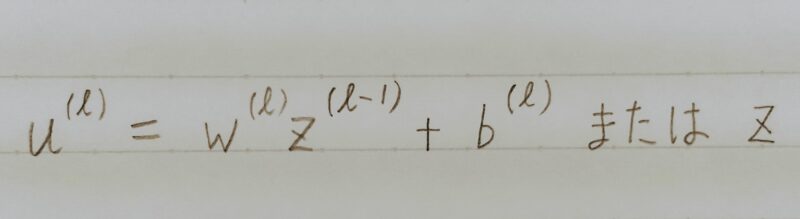


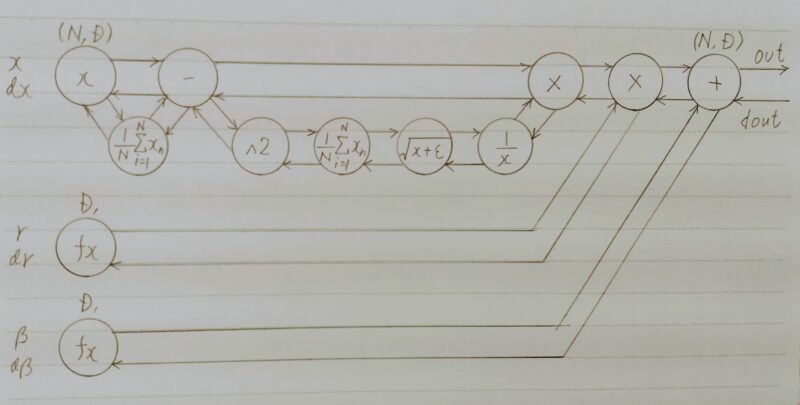
※Batch Normalization の処理手順
Normalizationの条件に入っている場合:現在のバッチの平均・分散を使用
Normalizationの条件に入っていない場合:学習した移動統計の平均・分散を使用
学習率の最適化手法
●深層学習の目的
学習を通して誤差を最小にするネットワークを作成すること
→ 誤差E(w)を最小化するパラメータwを発見すること
⇒ 勾配降下法を利用してパラメータを最適化
【勾配降下法】
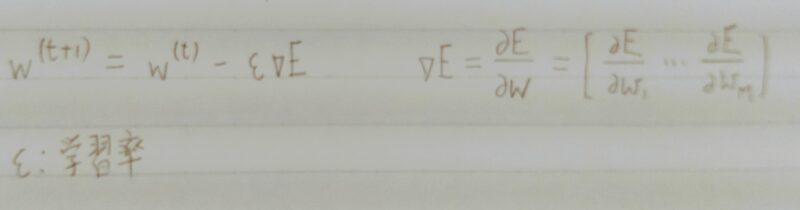
| 学習率が大き過ぎた場合 | 学習率が小さ過ぎた場合 | |
|---|---|---|
| 状態 | 最小値にいつまでも辿り着かず発散してしまう。 | ・収束するまでに時間がかかってしまう。 ・大域局所最適値に収束しづらくなる。 |
〈初期の学習率設定方法の指針〉
- 初期の学習率を大きく設定し、徐々に学習率を小さくしていく
- パラメータ毎に学習率を可変させる。
⇒ 学習率の最適化手法を利用して学習率を最適化
- 勾配降下法(SDG)
・課題:勾配が振動してしまい非効率なパラメータ探索をしてしまう。 - Momentum
・工夫:モーメンタム係数μにより勾配の振動を抑制/変化の加速
・課題:最適化に重要なパラメータと重要ではないパラメータを一律に最適化をしてしまう
・NAG(Nesterovの加速勾配法)はMomentumの一種 - AdaGrad
・工夫:個別のパラメータ方向に応じて学習率を補正&過去の勾配成分を利用
・課題:学習率が徐々に小さくなるので、鞍点問題を引き起こすことがあった。 - RMSrop
・工夫:勾配の大きさに応じて学習率を調整(指数移動平均を蓄積) → 鞍点問題を解決 - Adam
・工夫:MomentumとAdaGradをヒントに1次と2次のモーメント推定に着目 - AdaDelta
・工夫:ニュートン法を勾配降下法で近似することによりロバストな学習率を実現
Momentum(モメンタム)

| Momentum | 勾配降下法 | |
|---|---|---|
| 特徴 | 誤差Eを重みwで微分したものと学習率εの積を減算した後、現在の重みwtに前回の重みwt-1を減算した値と慣性の積を加算する。 | 誤差Eを重みwで微分したものと学習率εの積を減算する。 |
- SGDに慣性項(Momentum)を付与した手法
(最適化に向けた移動に「慣性」をつける。) - 同じ方向に移動していく場合はどんどん加速し、逆方向に進もうとすると「慣性」により減速する。
- μ:慣性(Momentum)係数
・ハイパーパラメータ
・慣性項の強さを決める係数
・重みパラメータの揺れ(振動)を緩やかにするための係数(重みパラメータの更新経路が緩やかになる)
| 最適化手法 | メリット | デメリット |
|---|---|---|
| Mometum | ・大域的最適解となる。 ・谷間についてから最も 低い位置(最適値) にいくまでの時間が早い。 | 最適化が難しい (ハイパーパラメータが 2つあるため) |
ハイパーパラメータ(英語:Hyperparameter)とは機械学習アルゴリズムの挙動を設定するパラメータをさします。少し乱暴な言い方をすると機械学習のアルゴリズムの「設定」です。
引用元:codexa
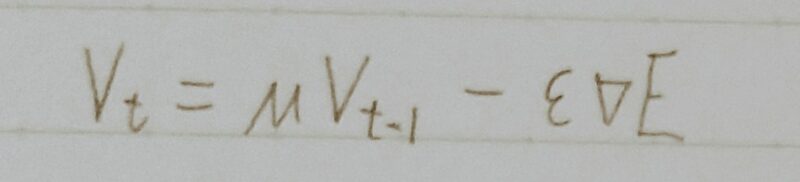
self.v[key] = self.momentum * self.v[key] – self.learning_rate * grad[key]
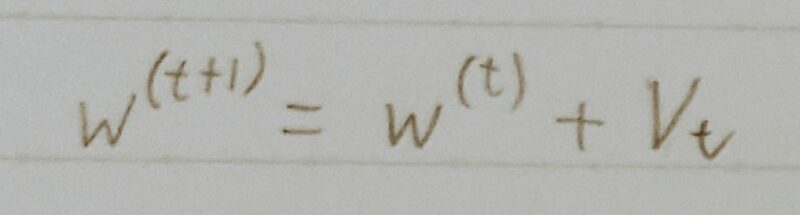
params[key] += self.v[key]
慣性:μ
NAG(Nesterovの加速勾配法)
- Mometum係数μにより勾配の振動を抑制/変化の加速
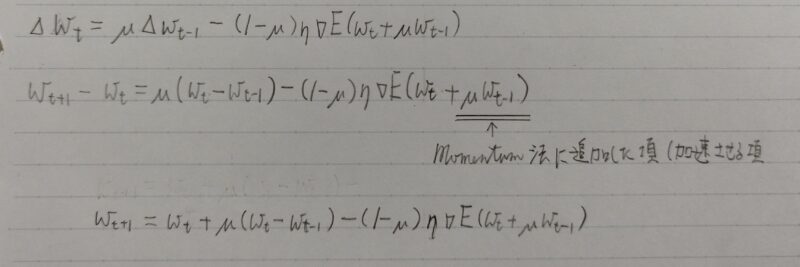
AdaGrad
最適化に重要なパラメータと重要ではないパラメータを一律に最適化をしてしまう。
勾配のアダマール積を蓄積し、すでに大きくアップグレードされたパラメータほど更新量を小さくする。
数学におけるアダマール積(英: Hadamard product)は、同じサイズの行列に対して成分ごとに積を取ることによって定まる行列の積である。要素ごとの積(英: element-wise product)、シューア積(英: Schur product)、点ごとの積(英: pointwise product)、成分ごとの積(英: entrywise product)などとも呼ばれる。
引用元:Wikipedia
- 学習が進むほど学習率を小さくしていく手法
・パラメータが最適値まで遠い時(学習初期)
⇒ パラメータ更新量を大きく
・パラメータが最適値に近づいた時(学習終盤)
⇒ パラメータ更新量を小さく - パラメータ方向に応じて学習率を補正
- 過去の勾配成分を利用(勾配のアダマール積を蓄積)

| AdaGrad | 勾配降下法 | |
|---|---|---|
| 特徴 | 誤差Eを重みwで微分したものと再定義した学習率(ε・1/√ht)の積を減算する。 | 誤差Eを重みwで微分したものと学習率εの積を減算する。 |
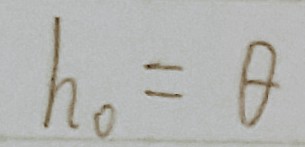
↑ 何かしらの値でhを初期化
self.h[key] = np.zeros_like(val)
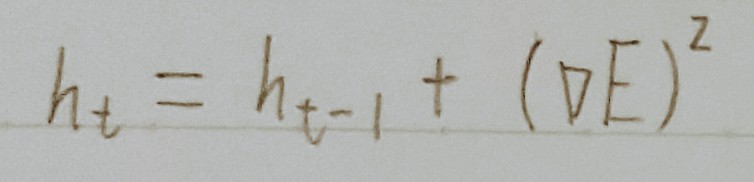
↑ 計算した勾配の2乗を保持
self.h[key] += grad[key] * grad[key]
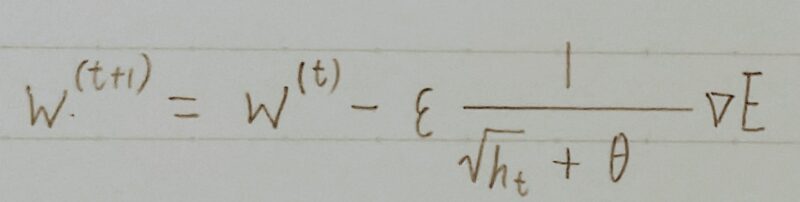
↑ 現在の重みを適応させた学習率で更新
params[key] = self.learning_rate * grad[key] / (np.sqrt(self.h[key]) + 1e-7)
- 学習率低下の性質が単調
学習初期の段階で学習率が過度に小さくなると収束するまで時間がかかり、局所的最適解から抜け出せなくなることがある。(鞍点問題) - 一旦、更新量が飽和してしまうと重みが更新されなくなる。
↓改善
RMSProp
鞍点問題・・・鞍点とはある次元から見ると極小に見え、次の次元から見ると極大となるものを指します。機械学習において誤差関数に鞍点が生じてしまうと、実際は最小値に到達していないにもかかわらず、勾配が0となってしまうため学習が止まってしまう問題が生じてしまいます。
引用元:zeroone
RMSProp
- 2012年にTijmen Tielemanらが提唱した手法
- AdaGradを改良したアルゴリズム
勾配の2乗の指数移動平均を取るように変更 - 指数的な移動平均vi,t(減衰率:ρ)←更新量が0から戻らない問題を解決
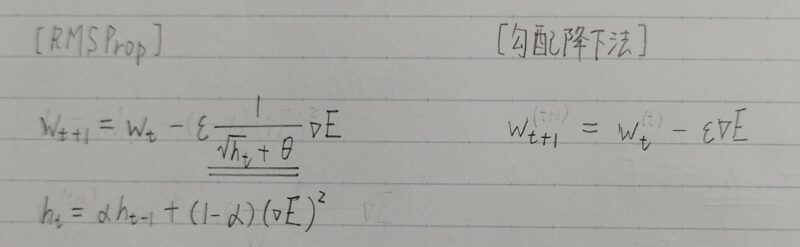
| RMSProp | 勾配降下法 | |
|---|---|---|
| 特徴 | 誤差Eを重みwで微分したものと最定義した学習率(ε・1/(√ht+θ))の積を減算する。 | 誤差Eを重みwで微分したものと学習率の積を減算する。 |
- 勾配の指数移動平均を採用
AdaGradが「過去の全ての勾配の平均」をとるのに対して、RMSPropは「指数移動平均」を採用 - αが新たに登場
α:過去の勾配による影響を減衰させるパラメータ - AdaGradからの最大の変更点
αによって過去の勾配の影響を抑えると共に、htを優先して反映させる効果を狙っている。→より直近の勾配情報を優先して計算
- 局所的最適解にはならず、大域的最適解となる。
- ハイパーパラメータの調整が必要な場合が少ない。
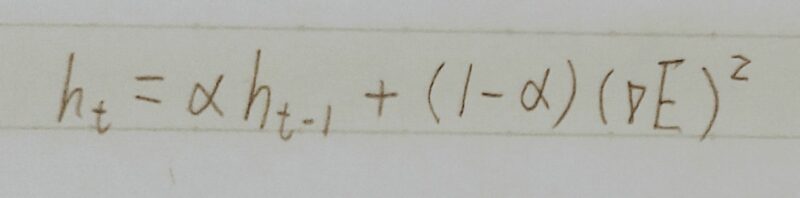
self.h[key] *= self.decay_rate
self.h[key] += (1 – self.decay_rate) * grad[key] * grad[key]
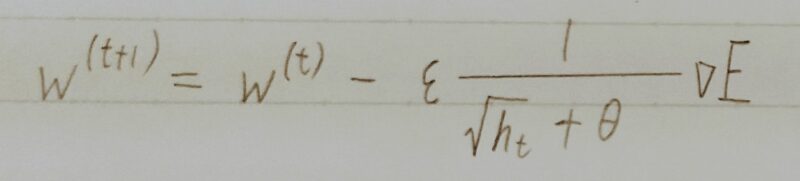
params[key] -= self.learning_rate * grad[key] / (np.sqrt(self.h[key]) + 1e-7)
Adam
- 非常によく利用される
- Adamのメリット
Momentum、RMSPropの各々のメリットを活かしたアルゴリズム
Momentum:過去の勾配の 指数関数的減衰平均
RMSProp :過去の勾配の2乗の指数関数的減衰平均 - 重みの更新式
Wt+1=wt – αΔwL(w)
α:RMSPropの要素
ΔwL(w):モーメンタムの要素誤差関数の値をより小さくする方向に重みWとバイアスbを更新 ⇒ 次の周(エポック)の周(エポック)に反映

出典元:Adam: A Method for Stochastic Optimization (arxiv.org)
AdaDelta
- ニュートン法を勾配降下法で近似することによりロバストな学習率を実現
(学習率ηを用いない)
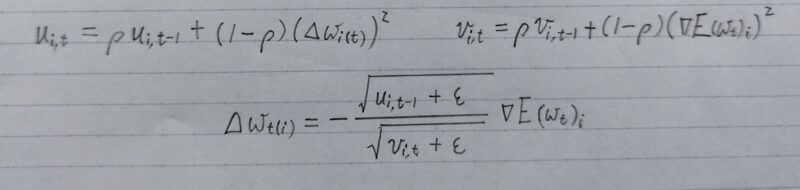
ニュートン法とは・・・
f(x)=0になるようなxを求めるアルゴリズムの1つで、方程式の解を近似的に求めることができる方法引用元:「ウィキペディア」
過学習
テスト誤差と訓練誤差とで学習曲線が乖離すること→ 特定の訓練サンプルに対して、特化して学習する
- パラメータの数が多い
- パラメータの値が適切ではない
⇒ネットワークの自由度(層数、ノード数、 - ノードが多い、パラメータの値が高いetc・・・
ネットワークの自由度(層数、ノード数、パラメータの値etc・・・)を制約すること⇒ 正則化手法を利用して過学習を抑制する
- L1正則化、L2正則化
- ドロップアウト
- Weight decay(荷重減衰)
L1正則化(ラッソ回帰)、L2正則化(リッジ回帰)
重みが大きい値をとることで、過学習が発生することがある。⇒ 学習させていくと、重みにばらつきが発生する。重みが大きい値は、学習において重要な値であり、重みが大きいと過学習が起こる。
誤差に対して、正則化項を加算することで、重みを抑制する⇒ 過学習が起こりそうな重みの大きさ以下で重みをコントロールし、かつ重みの大きさにばらつきを出す必要がある。

- L1正則化 → ラッソ回帰
- L2正則化 → リッジ回帰
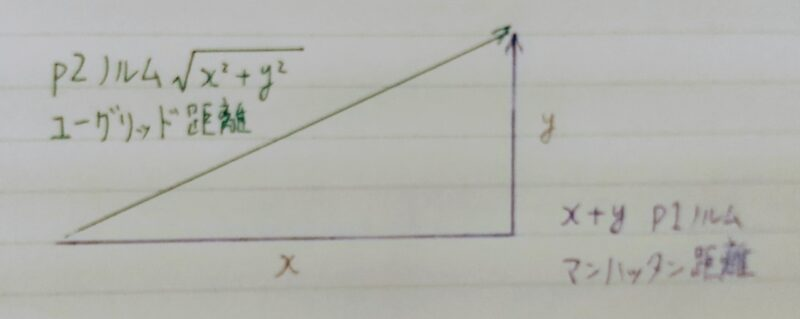
P2ノルムは距離を正確に表しているが計算量が多いため、少ない計算量で距離を表す方法としてP1ノルムが用いられる。
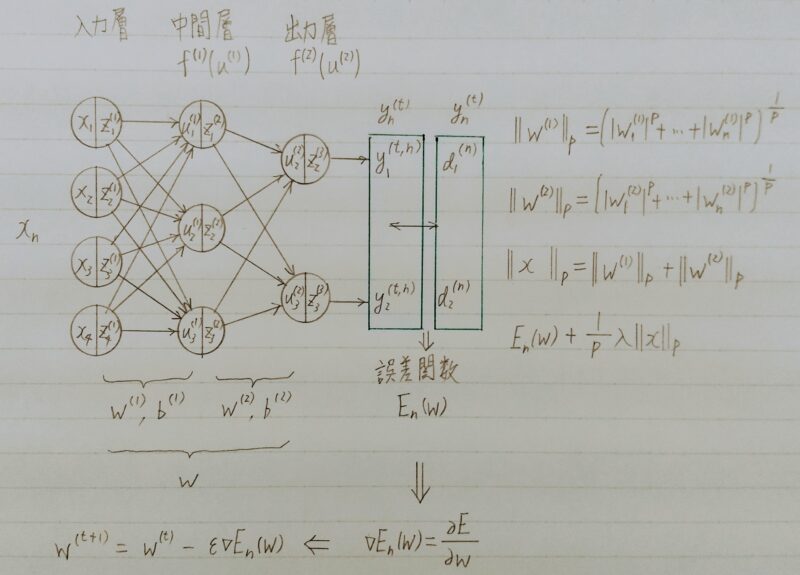
数式とコード
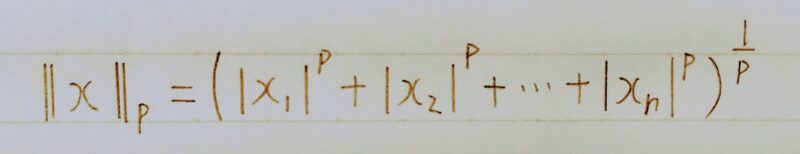
np.sum(np.abs(network.params[‘W’ + str(idx)]))
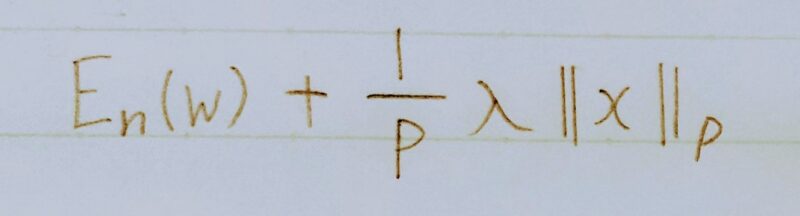
weight_decay += weight_decay_lambda
*np.sum(np.abs(network.params[‘W’ + str(idx)]))
loss = network.loss(x_batch, d_batch) + weight_dacay
例題チャレンジ
L2パラメータ正則化
深層学習において、過学習の抑制・汎化性能の向上のために正則化が用いられる。その一つにL2ノルム正則化(Ridge Weigh Decay)がある。以下はL2正則化を適用した場合に、パラメータの更新を行うプログラムである。あるパラメータparamと正則化がないときにそのパラメータに伝播される誤差の勾配gradが与えられたとする。
最終的な勾配を計算する(え)にあてはまるものはどれか。ただし、rateはL2正則化の係数を表すとする。
def ridge(param, grad, rate):
“””
param: target parameter
grad: gradients to param
rate: ridge coefficient
“””
grad += rate * (え)
(1) np.sum(param**2)
(2) np.sum(param)
(3) param**2
(4) param
解答 (4)param
【解説】L2ノルムは、||param||2なのでその勾配が誤差の勾配に加えられる。つまり、2*paramであるが、係数2は正則化の係数に吸収されても変わらないのでparamが正解である。
L1パラメータ正則化
以下はL1ノルム正則化(Lasso)を適用した場合に、パラメータの更新を行うプログラムである。あるパラメータparamと正則化がないときにそのパラメータに伝播される誤差の勾配gradが与えられたとする。
最終的な勾配を計算する(お)にあてはまるものはどれか。ただし、rateはL1正則化の係数を表すとする。
def lasso(param, grad, rate):
” ” ”
param: target parameter
grad: gradients to param
rate: lasso coefficient
” ” “
x = (お)
grad += rate * x
(1) np.maximum(param, 0)
(2) np.minimum(param, 0)
(3) np.sign(param)
(4) np.abs(param)
解答 (3) np.sign(param)
【解説】L1ノルムは、|param|なのでその勾配が誤差の勾配に加えられる。つまり、sign(param)である。signは符号関数である。
補足)sign(x)の説明
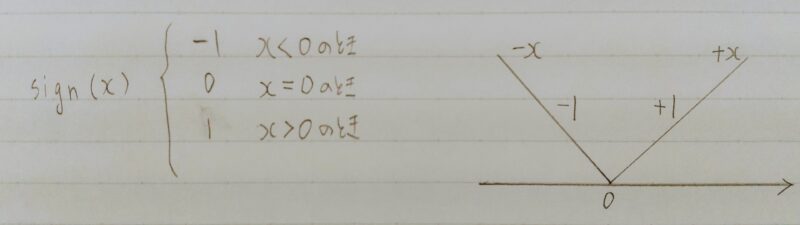
Dropout(ドロップアウト)
- 過学習の課題:ノード数が多い
- 課題解決の方法:ランダムにノードを削除して学習させること
- メリット:データ量を変化させずに、異なるモデルを学習させていると解釈できる
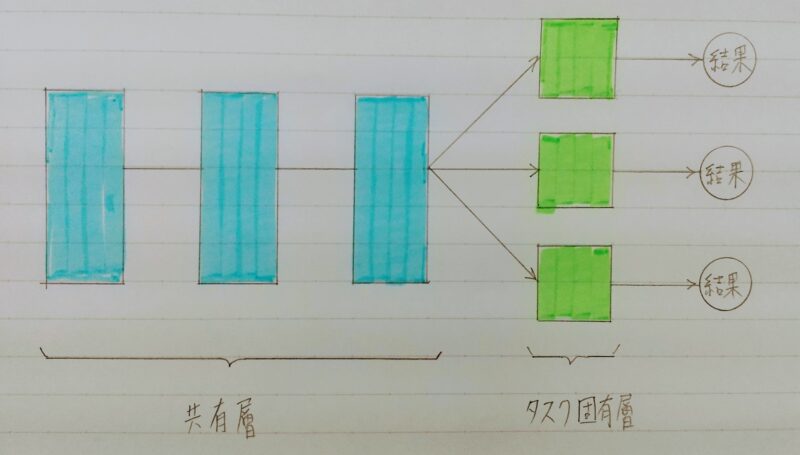
マルチタスク
マルチタスク学習の仕組み
- マルチタスク学習とは・・・複数の問題を単一のモデルでまとめて解く手法
(アンサンブル学習も同様) - 対比される学習手法としてシングルタスク学習がある。
| 学習手法 | 概要 |
|---|---|
| シングルタスク学習 | ・1つの問題に対して1つのモデルで解決 ・モデル数と解決対象の問題数が1対1 ・解決対象の問題数に対してモデル数が増加 |
| マルチタスク学習 | ・複数の問題に対して1つのモデルで解決 ・モデル数と解決対象の問題数が1対N |
マルチタスク学習の仕組み
| メリット | デメリット |
|---|---|
| モデル数が少なくて済む | 単一のタスクだけに着目するとより多くのメモリ・演算量が必要 |
| 各タスクの相乗効果により、それぞれのタスクで性能向上が期待できる | 学習の難易度が高い |
| 学習時間や総パラメータ数が減らせる |
マルチタスク学習の適用例
- 画像認識分野
クラス分類
物体検出(Mask RーCNN 等) - 自然言語分野
MLM(穴埋め問題)
NSP(文章推測問題)
アンサンブル学習
複数の学習させた複数モデルを融合させて1つの学習モデルを生成する手法

「アンサンブル」の意味は「合奏曲」などだよ。
この「合奏曲」をイメージすると分かりやすいよ!!
バギング(bagging)
- 並列に複数の学習器を構築し、それぞれの学習器の結果を用いて総合的な出力結果を求める手法。なお学習データは一部のみ使用。
- 回帰の場合:出力結果は平均値
- 分類の場合:出力結果は多数決

「バギング(bagging)」の意味は「袋詰め」だよ。
(「バッグ(bag)」は「袋」)
この「袋詰め」をイメージすると分かりやすいよ!!
バギングは以下の手順で行う。
- ①学習データから決められた回数分のデータを抽出し、それぞれデータセットを作る。
- ②データセットからモデルを作る
- ③上記①~②を決められた回数繰り返す
- ④作成した学習器から結果を構築する
- バギングと決定木を組み合わせた手法をランダムフォレストと言う。
- ランダムフォレストで使用する学習器は決定木モデルとなる。
| メリット | デメリット |
|---|---|
| データの一部を訓練データとして使うことで、 バリアンス(予測値のばらつき度合い)を抑えることができ、それにより過学習を抑制できる | データを使いすぎるとバリアンスが高くなり、過学習の原因となる 補足)バリアンスとはモデル予測の広がりを示す値のこと |
| それぞれ並列で計算できるため、処理時間を少なくすることができる | 訓練データが似通った特徴の場合、テストデータによる検証時に精度向上が期待できない場合がある |
ブースティング(boosting)
■バギングが並列なのに対し、ブースティングは直列的に学習する。

「ブースティング(boosting)」の意味は「押し上げ」だよ。
この「押し上げ」をイメージすると分かりやすいよ!!
■ブースティングは以下のような流れとなる。
- ①データを決められた回数分抽出して学習器を作成する
- ②学習器で生成した誤った結果と正解のサンプルを比較する
- ③誤り率と重要度を学習器ごとに計算し、全体の重みを調整する
| メリット | デメリット |
|---|---|
| 一つ前の学習器で生成したデータを再利用するため、バギングより精度向上が期待できる。 | バリアンスが高くなり易く、過学習が起こりやすい。 |
スタッキング(stacking)
様々なアルゴリズムを使用して精度を上げる手法

「スタッキング(stacking)」の意味は「積み重ねること」だよ。
この「積み重ねること」をイメージすると分かりやすいよ!!
- 学習器にランダムフォレストや勾配ブースティングなどの様々な計算法を使って、複数のモデルを用意する
- 各々のモデルからそれぞれ予測値を出力する
- 各予測値をまとめたメタモデル(Meta Model)を作成する
- メタモデルから最終予測値を作成する

「メタモデル」の意味が分からない?

「メタ(Meta)」とは「超越」を意味する。
だから「メタモデル(Meta Model)」は超越したモデルすなわち「モデルのモデルとなるもの」だよ。
| メリット | デメリット |
|---|---|
| 様々な計算方法を目的に合わせて使用できるので、精度が上がり易くなる | 様々な計算方法を目的に合わせて使用する必要があるため、手間がかかる |
確認テスト
- Q1.

- A1.
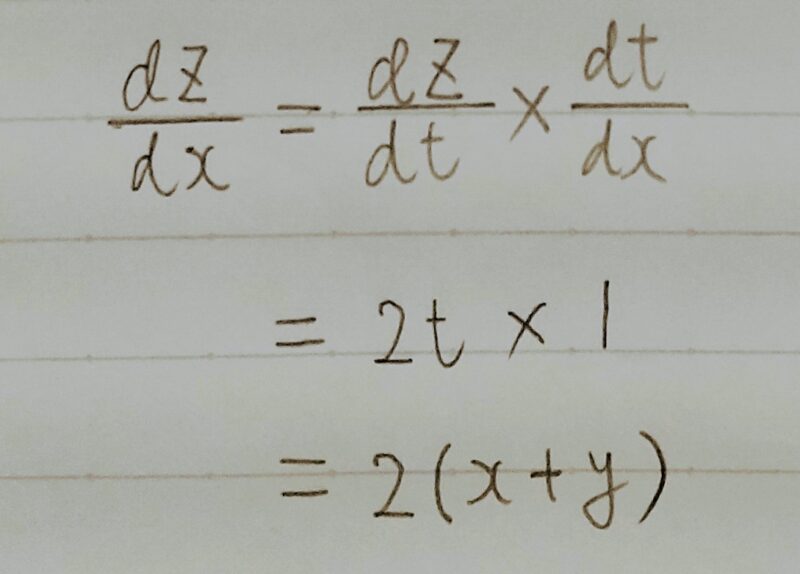
問題の解答
- Q2.シグモイド関数を微分した時、入力値が0の時に最大値をとる。その値は求めよ。
- A2.0.25(グラフ参照)
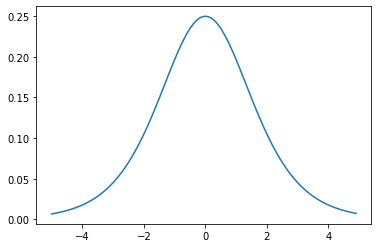
- Q3.重みの初期値に0を設定すると、どのような問題が発生するか。簡潔に説明せよ。
- A3.重みを0で初期化すると正しい学習が行えない。
→全ての重みの値が均一に更新されるため、多数の重みを持つ意味がなくなる。
- Q4.下図について、L1正則化を表しているグラフはどちらか答えよ。
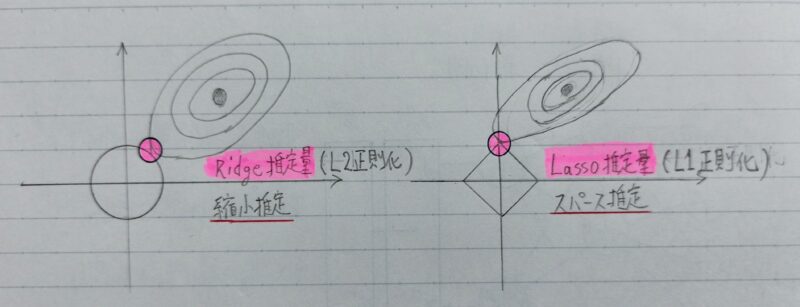
- A4.上記の右のグラフがL1正則化
まとめ

最後まで読んで頂きありがとうございます。
皆様のキャリアアップを応援しています!!

コメント