- 「主成分分析」について学びたいけど理解できるか不安・・・
- 「主成分分析」についてどこから学んでいいか分からない?
- 「主成分分析」を分かりやすく教えて!
「主成分分析(PCA:Principal component analysis)」は、機械学習において説明変数を何にするか決める時に利用するもので、説明変数の数が減り、計算量が減少しまた過学習を防止することが期待できるものですが、理解できないケースは非常に多いです。
私は過去に基本情報技術者試験(旧:第二種情報処理技術者試験)に合格し、また2年程前に「一般社団法人 日本ディープラーニング協会」が主催の「G検定試験」に合格しました。現在、「E資格」にチャレンジ中ですが3回不合格になり、この経験から学習の要点について学ぶ機会がありました。
そこでこの記事では、「主成分分析」のポイントを解説します。
この記事を参考に「主成分分析」が理解できれば、E資格に合格できるはずです。
アウトライン
- 主成分分析(PCA:Principal component analysis)
- 多変量データを持つ構造をより少数個の指標に圧縮
・変数の個数を減らすことに伴う、情報の損失はなるべく小さくしたい
・少数変数を利用した分析や可視化(2・3次元の場合)が実現可能 - 主成分の数の最大値はデータの特徴量の数である。
一般に可視化の際は、主成分の数を3以下にすることが多い。
主成分の数が少ないほど、データを射影した際に情報が落ちる
AIモデルにおいて説明変数を何にするか決める時、主成分分析を利用することで説明変数の数が減り、計算量が減少しまた過学習を防止することが期待できる。
数学的定式化
データ形式の説明
学習データ: xi = (xi1,xi2,・・・,xim) ∈ R
平均(ベクトル): x = 1/n Σxi
データ行列: x = (x1-x,・・・,xn-x)T ∈ Rn×m
分散共分散行列: Σ = Var(X) =1/n(XTX)
↑ 〈復習〉【機械学習】統計学(期待値と標準偏差)とは?
分散: 各データと平均値との差の2乗
共分散:データx、yにおいて(xー平均値)×(yー平均値)の値


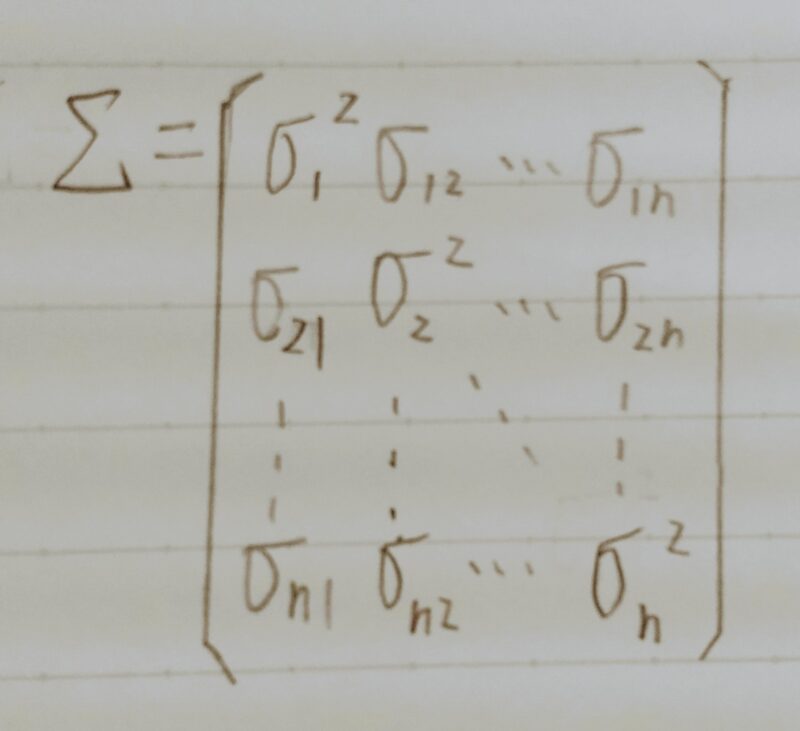
Q.2次元空間において「(-2,2),(-1,-1),(0,0),(1,1),(2,-2)」という5つのデータ点が与えられ、これらのデータに対して第1主成分と第2主成分へ射影した値を求めよ。
A.解答は次のとおり。
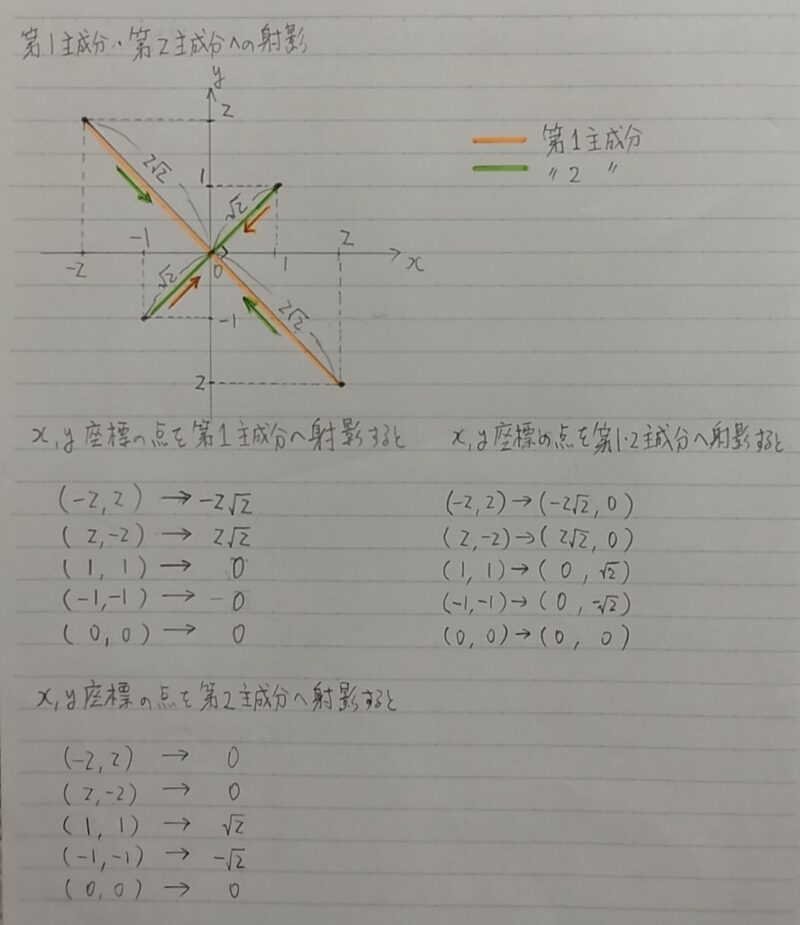
〈補足〉第1主成分ノルム及び第2主成分は(長さ)1に正規化される。
線形変換後のベクトル sj = (s1j,・・・,snj)T = Xaj aj ∈ Rm
※jは射影軸のインデックス
主成分分析の説明
- 係数ベクトルが変われば線形変換後の値が変化
〇情報の量を分散の大きさと捉える
〇線形変換後の変数の分散が最大となる射影軸を探索 - 以下の制約付き最適化問題を解く
〇ノルムが1となる制約を入れる(制約を入れないと無限に解がある)
目的関数 arg max aTjVar(X)aj 制約条件 ajTaj =1 - 制約付き最適化問題の解き方
〇ラグランジュ関数を最大にする係数ベクトルを探索(微分して0になる点)
ラグランジュ乗数
ラグランジュ関数 E(aj) = ajTVar(X)aj – λ(ajTaj – 1)
目的関数 制約条件 - ラグランジュ関数を微分して最適解を求める
- 元のデータの分散共分散行列の固有値と固有ベクトルが、
上記の制約付き最適化問題の解となる
微分 δE(aj)/δaj = 2Var(X)aj – 2λaj = 0 → 解 Var(X)aj = λ - 射影先の分散は固有値と一致
Var(s1) = a1TVar(X)a1 = λ1a1Ta1 = λ1 - 分散共分散行列は正定値対称行列 → 固有値は必ず0以上・固有ベクトルは直交
- 各主成分は互いに直交するように選ばれる
主成分と寄与率
- 分散共分散行列を計算
- 固有値問題を解く
- (最大)m個の固有値と固有ベクトルのペアが出現
K番目の固有値(昇順)並べ、対応する固有ベクトルを第k主成分と呼ぶ
分散共分散行列の最も大きい固有値が第1主成分の分散に一致する。
- 寄与率
〇第1~元次元分の主成分の分散は、元のデータの分散と一致
■2次元のデータを2次元の主成分で表示した時、固有値の和と元のデータの分散が一致
■第k主成分の分散は主成分に対応する固有値
Vtotal = Σλi
元データの 主成分の
総分散 総分散
〇寄与率:第k主成分の分散の全分散に対する割合(第k主成分が持つ情報量の割合)
〇累積寄与率:第1-k主成分まで圧縮した際の情報損失量の割合 - 再構成誤差
〇第1主成分から成る一次元空間へ射影したデータを再構成する場合と第1・第2主成分から2次元空間へ射影したデータを再構成する場合の再構成誤差を比較した場合、第1主成分から成る一次元空間へ射影した場合の方が再構成誤差が大きくなる。
実装演習
a.乳がんデータの分析主成分分析
- 設定
〇乳がん検査データを利用しロジスティック回帰モデルを作成
〇主成分を利用し2次元空間上に次元圧縮 - 課題
〇32次元のデータを2次元上に次元圧縮した際に、うまく判別できるかを確認
まとめ
最後まで読んで頂きありがとうございます。
皆様のキャリアアップを応援しています!!

コメント
コメント一覧 (2件)
Hi it’s me, I am also visiting this web site on a regular basis, this web site is actually nice and the people are actually sharing pleasant thoughts.
本ウェブサイトをご覧頂きありがとうございます。
投稿の励みになります。