- 「深層学習の安定化」について学びたいけど理解できるか不安・・・
- 「深層学習の安定化」についてその方法が分からない?
- 「深層学習の安定化」の方法について体系的に教えて!
「深層学習」において、その「学習の安定化(未学習・過学習の回避)」を図ることは、推定精度を向上させる上で重要ですが、興味があっても難しそうで何から学んだらよいか分からず、勉強のやる気を失うケースは非常に多いです。
私は過去に基本情報技術者試験(旧:第二種情報処理技術者試験)に合格し、また2年程前に「一般社団法人 日本ディープラーニング協会」が主催の「G検定試験」に合格しました。現在、「E資格」にチャレンジ中ですが3回不合格になり、この経験から学習の要点について学ぶ機会がありました。
そこでこの記事では、深層学習における学習の安定化を行う方法についてポイントを解説します。
この記事を参考にして「学習の安定化の方法」が理解できれば、E資格に合格できるはずです。
目次
過学習を抑制する方法
過学習が起きる原因とは・・・
過学習が起きる原因の例
- パラメータの数が多すぎる。
- パラメータの値が偏っている。 ← モデルが複雑すぎる
- ノードが多すぎる。 ← モデルが複雑すぎる
- 学習データが不足している。 ← モデルが複雑すぎる
- 学習データが偏っている。
- etc・・・
↓
過学習を抑制
| 正則化 | Dropout | 正規化 | |
|---|---|---|---|
| 内容 | ネットワークの自由度(層数、ノード数、パラメータの値、etc・・・)を制約する(Regularization) | ランダムにノードを削除して学習させる。 | レイヤー間を流れるデータの分布を、何らかの単位で平均が0、分散が1になるように正規化(Normalization) |
正則化
正則化の概要
正則化とは・・・
- ネットワークの自由度(層数、ノード数、パラメータの値etc・・・)を制約すること
引用元:【深層学習】性能向上の方法とは?
L1・L2正則化
過学習の解決策
- 誤差に対して正則化項を加算
- 重みを抑制
- 過学習が起こりそうな重みの大きさ以下で重みをコントロール
- 重みの大きさにばらつきを出す
- 重みを抑制

x:説明変数
w:回帰係数
λ:正則化係数
| L1正則化 | L2正則化 | |
|---|---|---|
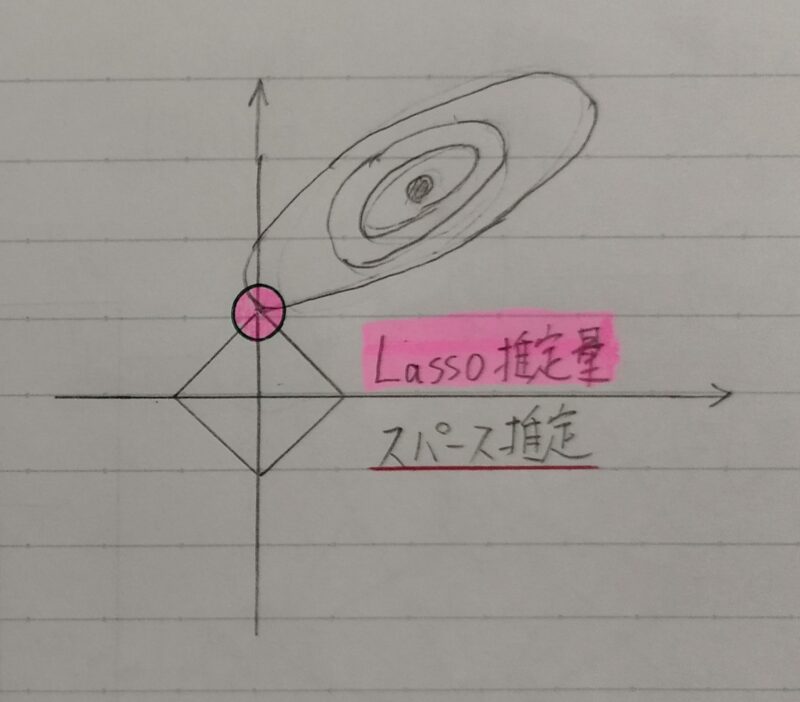
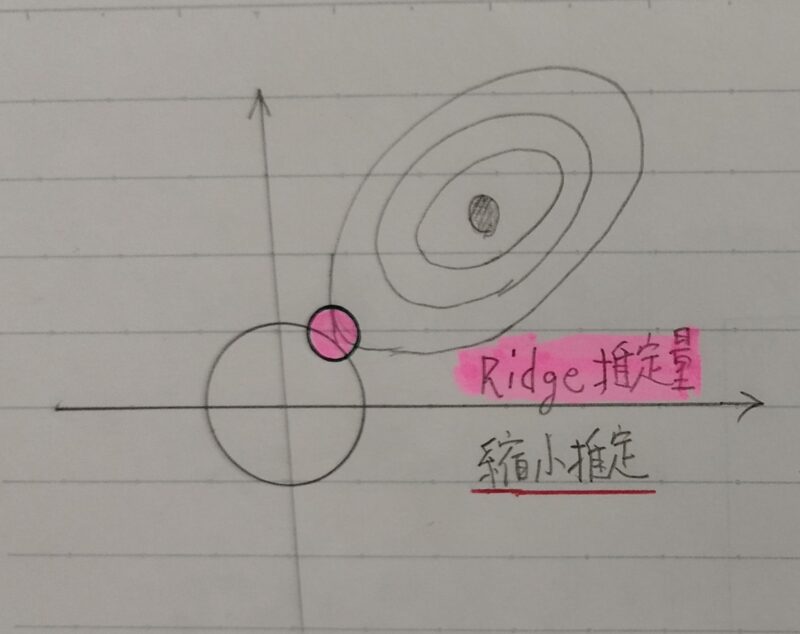
| 別名 | Lasso(ラッソ)回帰 | Ridge(リッジ)回帰 |
| 内容 | パラメータ自体を消滅 (スパース推定) | パラメータが発散することを抑制 (縮小推定) |
| 特徴 | いくつかの回帰係数は完全に0となる | いくつかの回帰係数は0に近づくが、 完全に0とはならない。 |
| 補足 | ロジスティック回帰モデル に適用可能 |
Elastic Net
Elastic Netとは・・・
- L1、L2正則化を組み合わせたもの。

- λ1、λ2:ハイパーパラメータ。各正則化項の制約の強さを調整する。
Dropout
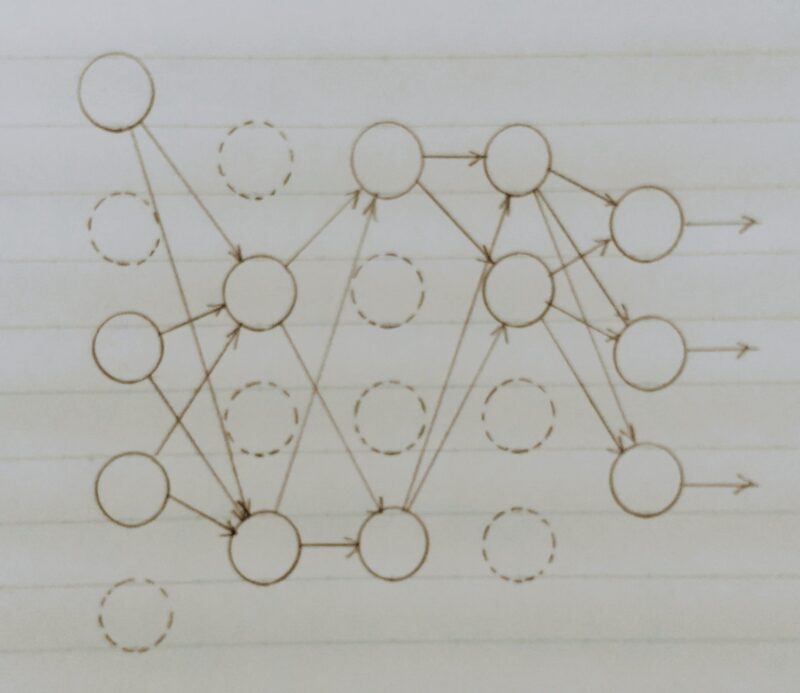
Dropoutとは・・・
- ランダムにノードを削除して学習させる。データ量はそのままで、より疎なモデルで学習することで過学習を抑制
正規化レイヤー
データの正規化(Normalization)とは・・・
レイヤー間を流れるデータの分布を、何らかの単位で平均が0、分散が1になるように正規化する。
引用元:https://arxiv.org/pdf/1803.08494.pdf
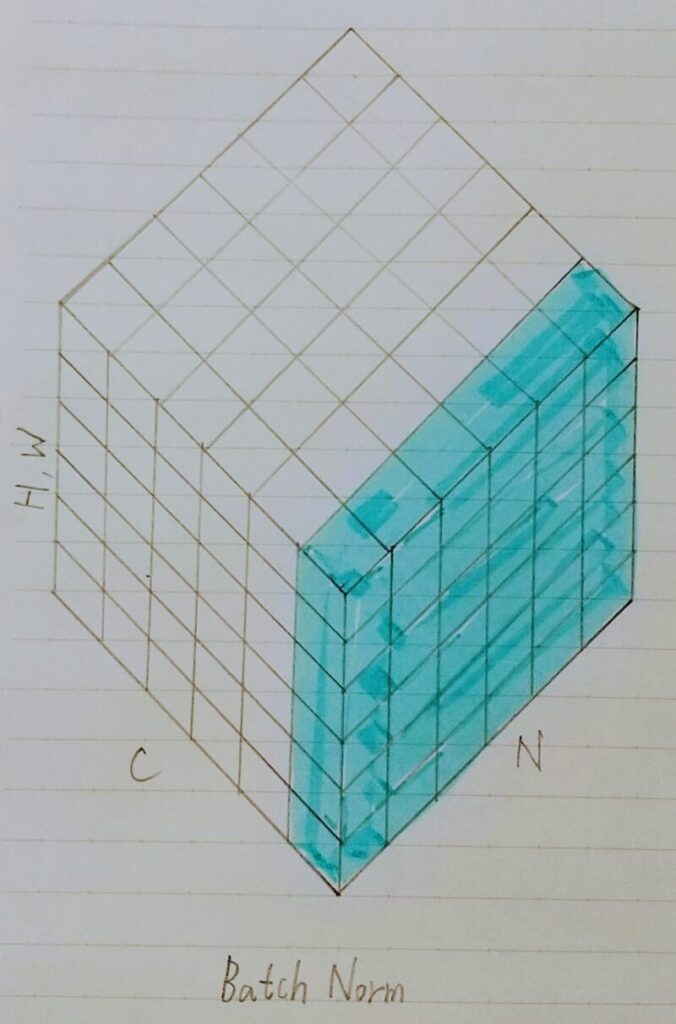
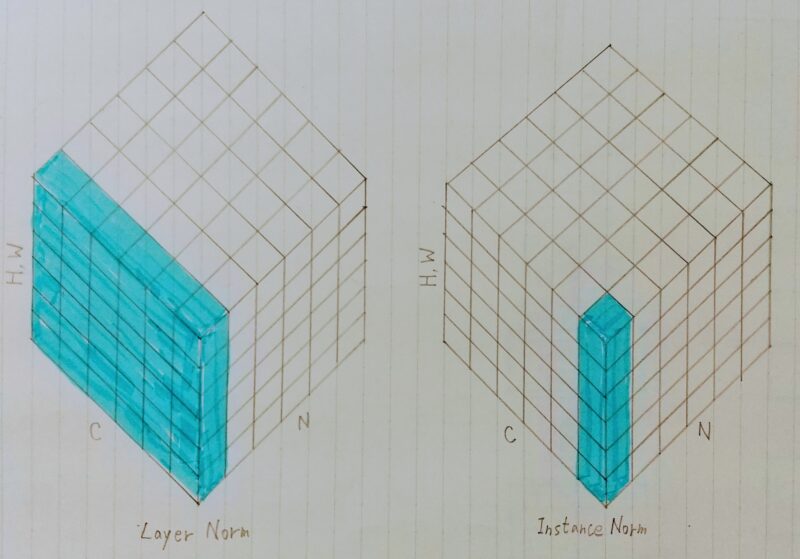
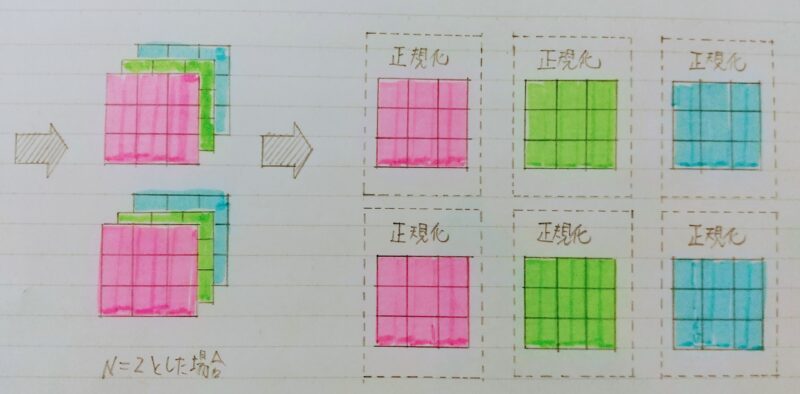
N:ミニバッチ数、C:Channel、H、W:Height/Width をまとめたもの
Batch正規化
Batch正規化(Batch normalization)とは・・・
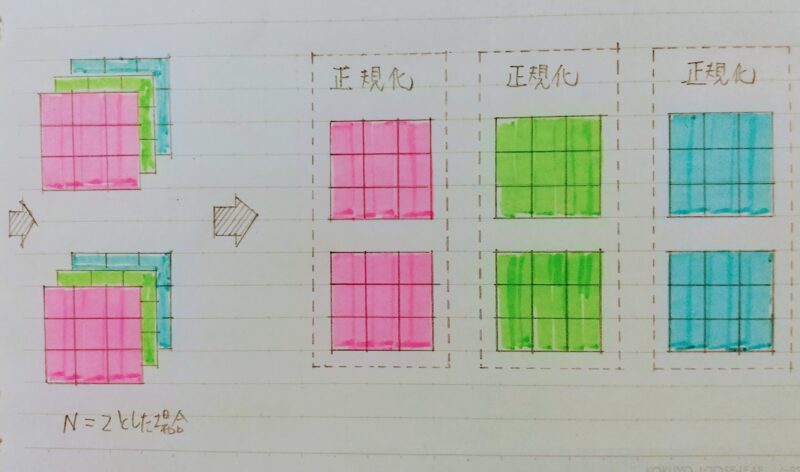
- ミニバッチ単位で、入力値のデータの偏りを抑制する手法
- H×W×CのsampleがN個あった場合に、N個の同一チャンネルが正規化の単位。
ブロック線図
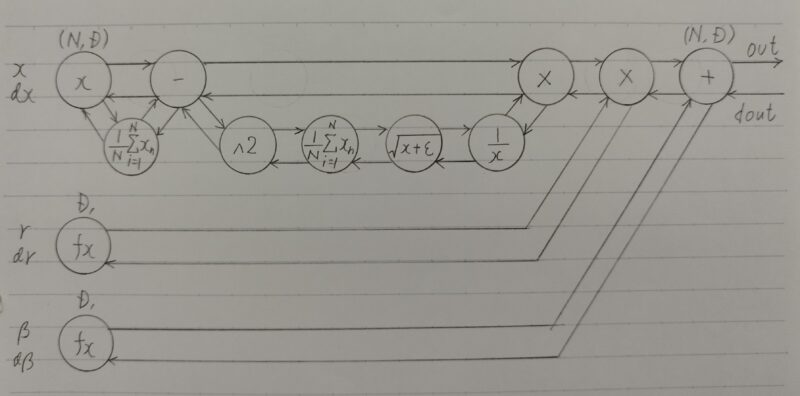
数学的記述


Batch正規化の課題
- ミニバッチのサイズが小さい場合には、効果が薄くなってしまう。
- 再帰型のモデルに適用したい場合、単純にバッチ平均が取れない。
(バッチの各要素ごとにSequence(順序)が異なるため)
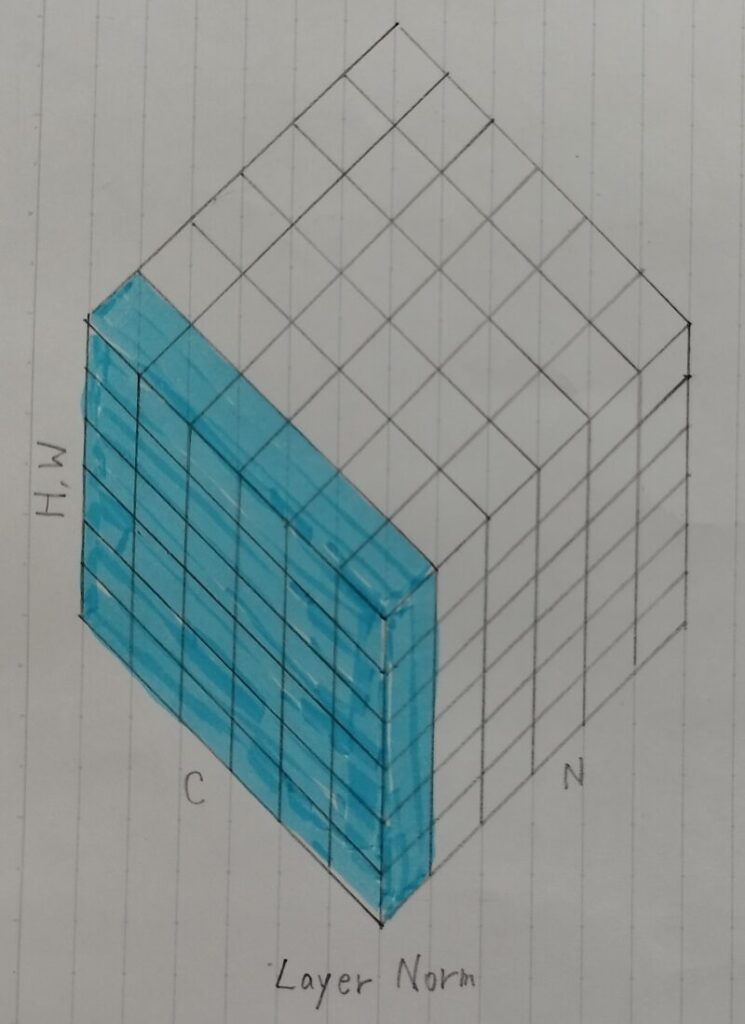
Layer正規化
Layer正規化(Layer normalization)とは・・・
- N個のsampleのうち1つに注目。H×W×Cの全てのpixelが正規化の単位。
- 単一サンプル の 各レイヤーの隠れ層の値 で正規化
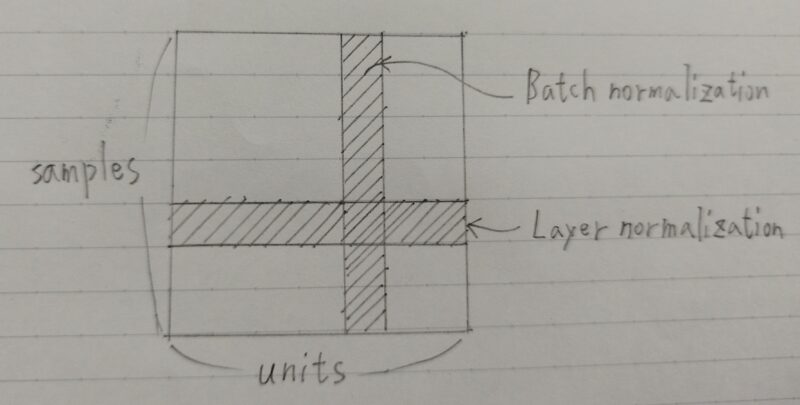
Batch正規化の課題の解決
- ミニバッチの数に依存しない
- 再帰型モデルに適用が可能
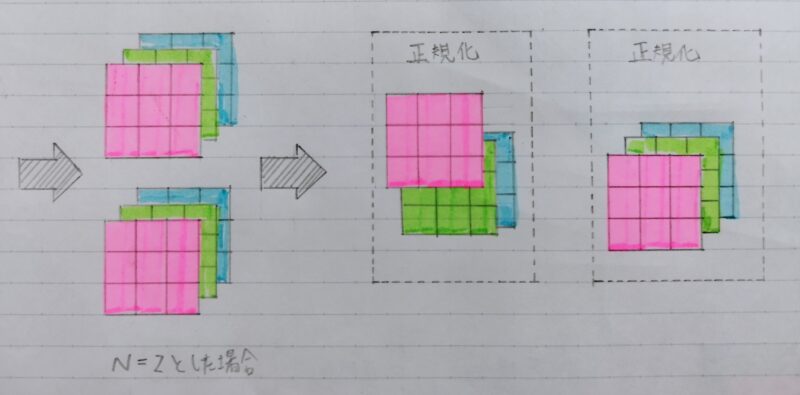
Layer正規化の計算式

- 訓練サンプルごとに独立に正規化パラメータを計算
⇒ バッチ正規化よりオンライン学習に適する - 各時間ステップで正規化パラメータを計算
⇒ 可変長入力データに対してロバスト
補足)ロバスト性:様々な外部の影響によって影響されにくい性質 - 訓練サンプルごとに独立に正規化パラメータを計算
⇒ 訓練時の計算方法=テスト時の計算方法
標準偏差σとは・・・
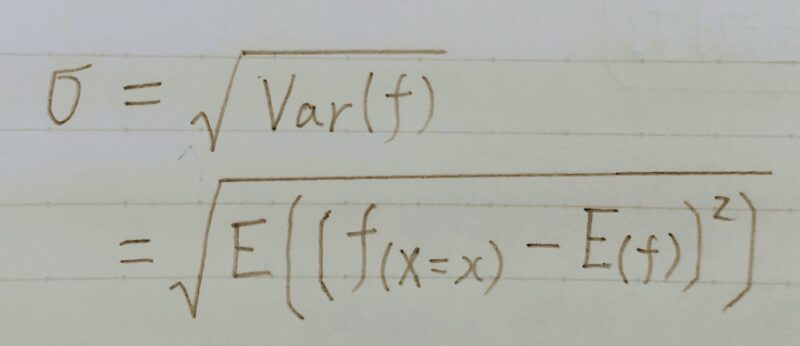
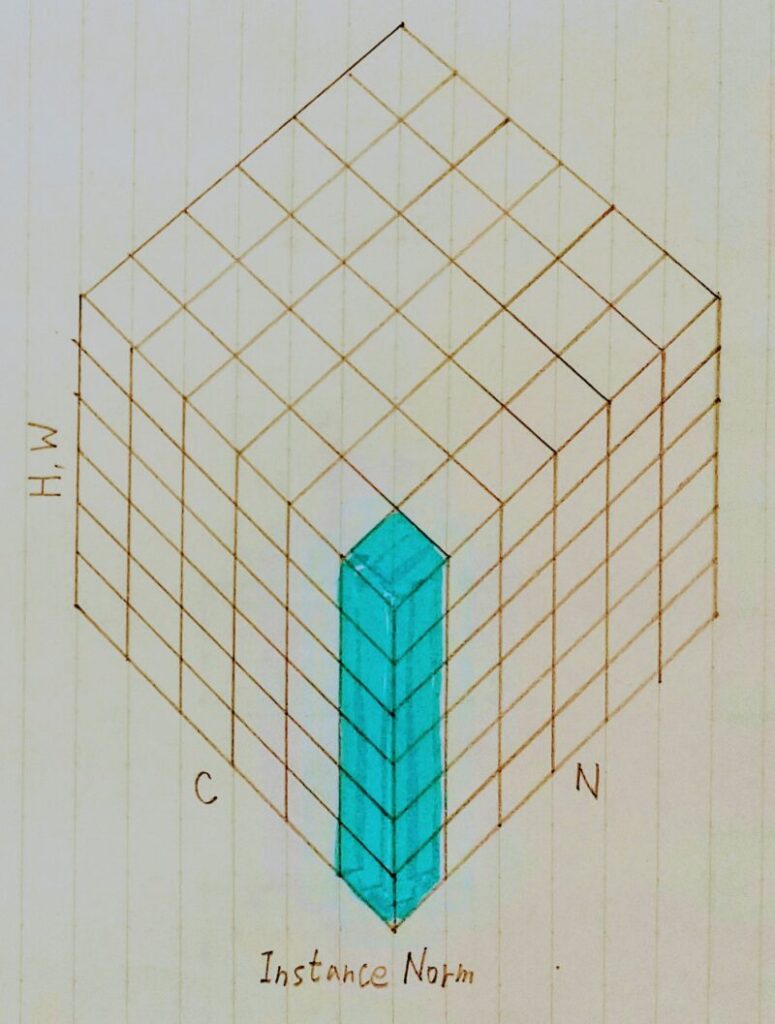
Instance正規化
Instance正規化とは・・・
- 各サンプルの各チャンネルごとに正規化。
- Batch正規化の際のバッチサイズが1の場合と等価。
実装演習
np.matmul(○,○) ← 内積をとる関数
np.mean(○,axis=1) ← 平均をとる関数
axis=1:列単位をとる

(編集中)
まとめ
最後まで読んで頂きありがとうございます。
皆様のキャリアアップを応援しています!!

コメント