- 「強化学習」について学びたいけど理解できるか不安・・・
- 「強化学習」についてどこから学んだらいいか分からない?
- 「強化学習」を体系的に教えて!
「強化学習」は長期的に報酬を最大化できるように環境の中で行動を選択できるエージェントを作ることを目標とする機械学習の一分野ですが、難しそうで何から学んだらよいか分からず、勉強のやる気を失うケースは非常に多いです。
私は過去に基本情報技術者試験(旧:第二種情報処理技術者試験)に合格し、2年程前に「一般社団法人 日本ディープラーニング協会」が主催の「G検定試験」に合格しました。現在、「E資格」にチャレンジ中ですが3回不合格になり、この経験から学習の要点について学ぶ機会がありました。
そこでこの記事では、「強化学習」を学習する際のポイントについて解説します。
この記事を参考に「強化学習」が理解できれば、E資格に合格できるはずです。
強化学習とは
- 機械学習
- 目標:
長期的に報酬を最大化できるように環境の中で行動を選択できるエージェントを作る - 仕組み:
行動の結果として与えられる利益(報酬)をもとに、行動を決定する原理を改善していく
強化学習の応用例
- 環境:
会社の販売促進部 - エージェント:
プロフィールと購入履歴に基づいて、キャンペーンメールを送る顧客を決めるソフトウェア - 行動:
顧客ごとに送信、非送信の二つの行動を選ぶことになる。 - 報酬:
以下の報酬を受ける。
負の報酬・・・キャンペーンのコスト
正の報酬・・・キャンペーンで生み出されると推測される売上
探索と利用のトレードオフ
環境について事前に完璧な知識があれば、最適な行動を予測し決定することは可能。
(上記の応用例:どのような顧客にキャンペーンメールを送信すると、
どのような行動を行うのかが既知である状況。)
↓
強化学習の場合、上記仮定は成立しないとする。
↓
不完全な知識を元に行動しながらデータを収集。
最適な行動を見付けていく。
| 探索が足りない状態 | 利用が足りない状態 | ||
|---|---|---|---|
| 結果 | 過去データでベストとされる行動のみを常に取り続ければ他に更にベストな行動を見付けることはできない。 | トレードオフ ⇔ | 未知の行動のみを常に取り続ければ、過去の経験が活かせない。 |
強化学習のイメージ
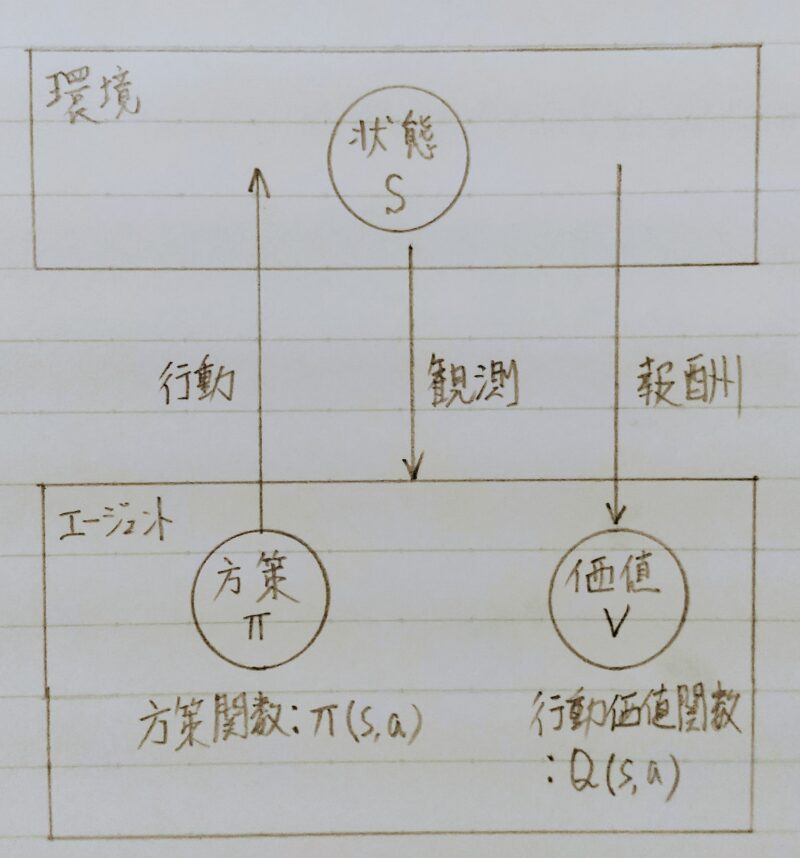
- 「エージェント」は主人公である。
- 会社で働くことをで例える。会社員(=エージェント)、会社(=環境)とすると、会社員は報酬を得るために仕事(=行動)する。どういった仕事をすればよいか(=方策)を検討するために会社の状況を観測し、また行動した結果(=行動価値関数)を参考にする。
強化学習の差分
- 目標が違う
| 強化学習 | 教師なし学習 教師あり学習 | |
|---|---|---|
| 目標 | 優れた方策を見付ける | ・データに含まれるパターンを見付け出す ・そのデータから予測する |
- 冬の時代があったが、計算速度の進展により大規模な状態をもつ場合の強化学習を可能としつつある。
- 「Q学習+関数近似法」手法の登場
- 行動価値関数:
行動する毎に更新して学習を進める方法
行動価値関数Q(s,a)を真の価値関数に近づけるように更新していく。 - 期待累積報酬和:
状態sにおいて行動aを選択し、その後方策πに従った場合の期待累積報酬和を得る。
- 価値関数や方策関数を関数近似する手法のこと
行動価値関数
| 行動価値関数 | 状態価値関数 | |
|---|---|---|
| 価値関数 | 状態と価値を組み合わせた価値に注目する (最近よく用いられている) | ある状態の価値に注目する |
方策関数
- 強化学習手法(方策ベース)において、ある状態でどのような行動を採るのかの確率を与える関数
- 方策関数:
π(s) = a - 関数の関係:
エージェントは方策に基づいて行動する。
π(s,a):VやQを基にどういう行動をとるか?
⇒経験を活かすorチャレンジする等 ⇒その瞬間、その瞬間の行動をどうするか?
Vπ(s):状態関数
}今の方策を続けた時の報酬の予測値が得られる
Qπ(s,a):状態+行動関数
⇒ やり続けたら最終的にどうなるか?
方策勾配法
- 方策をモデル化して最適化する手法
- とりうる状態や行動が離散値ではなく、連続値をとる場合にも適応可能である。
- 状態と行動の集合が有限で、かつマルコフ性を仮定すると、有限回の反復で最適な方策に収束する。
- θ(t+1)=θ(t)+εΔJ(θ) ε:学習率
- J(θ)とは「方策の良さ」← 定義しなければならない

上式はモンテカルロ近似(モンテカルロ法)により、以下の式に変形できる。
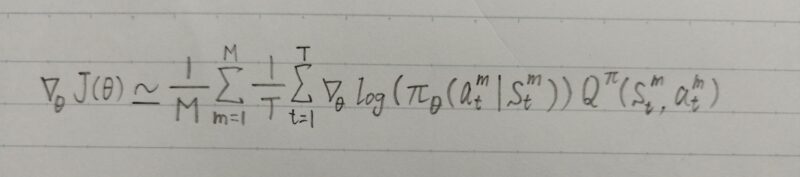
m:エピソードのイテレータ(反復子)
t:エピソード中のタイムステップのイテレータ(反復子)
※モンテカルロ近似(モンテカルロ法)とは・・・
引用元:biostatistics
- 複雑な数値計算を乱数を用いて近似解を求める方法の総称
- 例えばベイズ推定ではパラメータ数が多くなると、ベイズ推定式の分母の積分計算が非常に複雑になり、解けなくなる。このとき、分母の積分を正確に解く代わりに、乱数を使って近似解を求める方法が取られている。
上式で行動価値関数Qπ(stm,atm)を報酬Rtmで近似すると以下の形に変形できる。この近似を使い勾配を求めるアルゴリズムをREINFORCEアルゴリズムという。
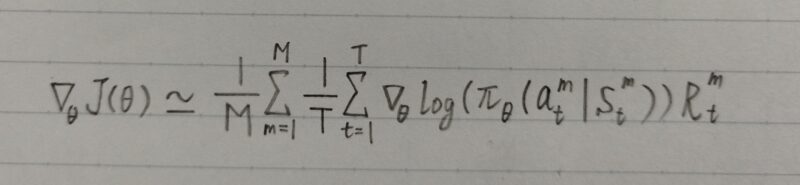
補足)REINFORCE・・・直訳すると「強化する」
- 価値関数Qの更新方法には上記、方策勾配法の他に「SARSA」がある。
| 方策勾配法(Q学習) | Sarsa | |
|---|---|---|
| 価値関数Qの更新方法 | ・オフポリシー(方策オフ手法) ・実際に進む行動(方策)と価値関数Qの更新に用いる行動(方策)が異なる。 | ・オンポリシー(方策オン手法) ・価値関数Qの更新は、次の行動状態から更新される実際の方策に従って価値を更新する。 |
深層Qネットワーク
- 深層Qネットワーク(Deep QーNetworks,DQN)
↑MDP(Markov decision process、マルコフ決定過程)を用いたQ学習に深層学習を適用
- 入力データ間に独立性がない(入力データが時系列データであるため)
- 更新されただけで選ばれる行動が大きく変わってしまう(価値関数が小さいため)
- 報酬のスケールが与えられたタスクによって大きく異なる
- 経験再生(Experience Replay)
①エージェントが経験した状態s、行動a、報酬r、および遷移先s´
→ 一旦メモリに保存
②損失の計算を行う際に、その保存した値からランダムサンプリングを行う。
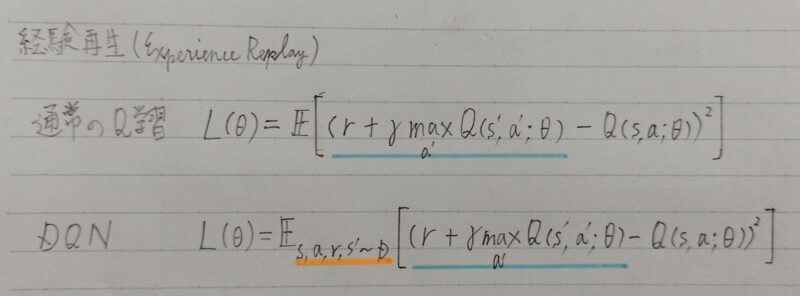
補足)経験再生を拡張した方法として、ランダムではなく各経験に優先順位をつけて経験を取り出す学習方法である「優先度付き経験再生(Prioritized Experience Replay,PER)」がある。
- 目標Qネットワーク(Target QーNetwork)の固定
問題:価値関数が小さく更新されただけでも選ばれる行動が大きく変わってしまう
目標値(教師信号)の算出に用いる行動価値関数Q(・)ネットワークのパラメータΘを固定し、一定周期でこれを更新することで学習を安定させる。
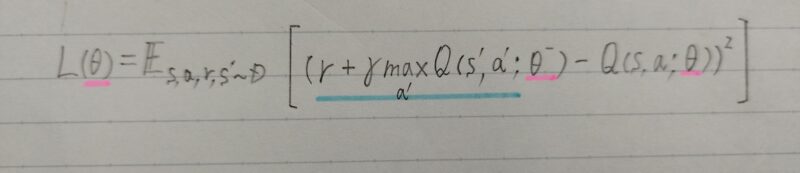
- 報酬のクリッピング(Reward Clipping)
報酬の値を統一すること。
報酬の値を{-1,0,1}の3値に制限する。
報酬の多寡情報が欠落するデメリットがあるが、安定して学習が進められるメリットの方が大きい。
例1)報酬をクリッピングをしない場合:
・金メダルを取ったら +100 point
・銀メダルをとったら +10 point
・対戦相手のパンチを食らったら -20 point
・対戦相手のキックを食らったら -50 point
例2)報酬のクリッピングをした場合:
・金メダルを取ったら +1 point
・銀メダルをとったら +1 point
・対戦相手のパンチを食らったら -1 point
・対戦相手のキックを食らったら -1 point
ベルマン方程式
- 価値を再帰的かつ期待値で表現する方法
- Vπ(s)=Σaπ(a|s)Σs’T(s’|s,a)(R(s,s’)+γVπ(s’))
rt+1+γVπ(st+1):価値
π(a|s):行動確率
T(s’|s,a):遷移状態確率
R(s,s’):報酬関数
行動の修正を行う方法
| モンテカルロ法 | TD法 | |
|---|---|---|
| 仕組み | 1エピソードの実績で修正を行う方法 | 1回の行動の直後に修正を行う方法 |
| 数式 | V(st) ← V(st)+a((rt+1+γrt+2+γ2rt+3+・・・+γT-1rT)ーV(st)) | V(st) ← V(st)+a(rt+1+γV(st+1)ーV(st)) |
| 正確性 | ○ | |
| 修正速度 | ○ |
※ TD法:Time Difference learning method(時間差分学習法)
まとめ
最後まで読んで頂きありがとうございます。
皆様のキャリアアップを応援しています!!

コメント