- 機械学習のうち「ロジスティック回帰モデル」について学びたいけど理解できるか不安・・・
- 「ロジスティック回帰モデル」についてどこから学んでいいか分からない?
- 「ロジスティック回帰モデル」のポイントを教えて!
「人工知能(AI:Artificial intelligence)」を勉強する際、その基礎である「機械学習」の考え方を理解していないため人工知能が理解できないケースは非常に多いです。
私は過去に基本情報技術者試験(旧:第二種情報処理技術者試験)に合格し、また2年程前に「一般社団法人 日本ディープラーニング協会」が主催の「G検定試験」に合格しました。現在、「E資格」にチャレンジ中ですが3回不合格になり、この経験から学習の要点について学ぶ機会がありました。
そこでこの記事では、機械学習のうち「ロジスティック回帰モデル」のポイントについて解説します。
この記事を参考にして「ロジスティック回帰モデル」が理解できれば、E資格に合格できるはずです。
<<「ロジスティック回帰モデル」のポイントを今すぐ見たい方はコチラ
ロジスティック回帰モデルの概要
- 分類問題(クラス分類)
・ある入力(数値)からクラスに分類する問題 - 分類で扱うデータ
・入力(各要素を説明変数または特徴量と呼ぶ)
・m次元のベクトル(m=1の場合はスカラ)
・出力(目的変数):0 or 1 の値
例)タイタニックデータ、IRISデータなど - パラメータの推定問題
・尤度最大化(最尤法)
数学的定式化
データ形式の説明
パラメータ:w=(w1,w2,・・・,wm)T∊Rm
線形結合:y=wTx+w0=Σj=1mwj+w0
ロジスティック回帰モデルの説明
- 分類問題を解くための教師あり機械学習モデル(教師データから学習)
- 入力とm次元パラメータの線形結合をシグモイド関数(Sigmoid function)に入力
- 出力はy=1になる確率の値になる
- 入力は実数・出力は必ず0~1に値
座標点(0,0.5)を基点(変曲点)として点対称でS(=σ:シグマ)字型曲線のグラフになる。
- 「クラス1に分類される」確率を表現
- 0~1の間を緩やかに変化する関数
・ステップ関数ではON/OFFしかない状態に対し、信号の強弱で伝えられるようになる
・予想ニューラルネットワーク普及のきっかけとなった。
・課題:大きな値では出力の変化が微小なため勾配消失問題を引き起こすことがあった。
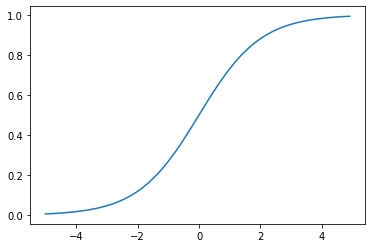
- パラメータが変わるとシグモイド関数の形が変わる
σ(x) = 1/(1+exp(ーax+b)) - aについて
・aを増加させると、x=0付近での曲線の勾配が増加
・aを極めて大きくすると、単位ステップ関数に近づく。
単位ステップ関数とは・・・
x<0でf(x)=0、x≧0でf(x)=1となるような関数 - bについて
・bの変化は段差の位置 → bを変化させると決定境界が変わる。 - 変化点について
・変化点とはax+b=0のときである。
なぜなら、変化点はσ(x)=0.5である。
一方、exp(0)=1でσ(x)=0.5となる。
故に変化点はax+b=0のときである。 - シグモイド関数の微分は、シグモイド関数自身で表現することが可能
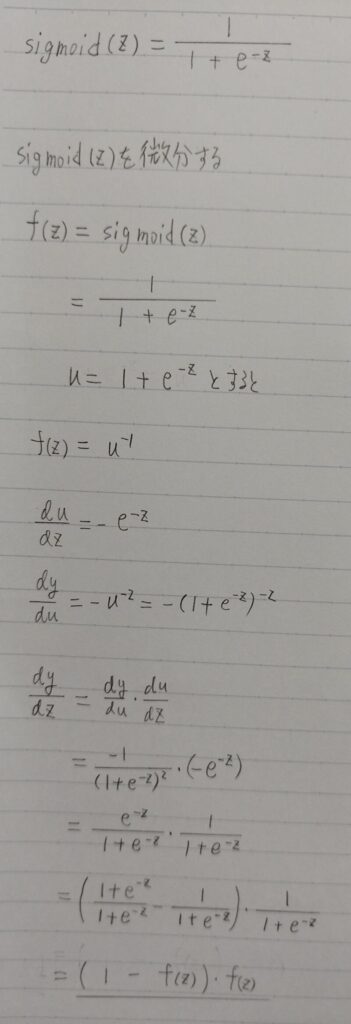
- 尤度関数の微分を行う際にこの事実を利用すると計算が容易
δσ(x)/δx = δ(1/(1 + exp(ーax))/δx
= σ(x)(1ーσ(x)) ← 連鎖率
「δσ(x)/δx」の最大値は 0.25
x=0の時、「δσ(x)/δx」が最大値をとり、σ(0)=0.5であるから
δσ(x)/δx =(1ー0.5)・(0.5)
=0.25
シグモイド関数の微分はシグモイド関数で表すことができる
- シグモイド関数の出力をY=1になる確率に対応させる
・データの線形結合を計算
・シグモイド関数に入力→出力が確率に対応
・[表記] i番目データを与えた時のシグモイド関数の出力をi番目のデータがY=1になる確率とする。 - 求めたい値
P(Y=1|X)=σ(w0+w1X1+・・・+wmXm) - 説明変数Xの実現値がデータのパラメーターに対する線形結合で与えられた際にY=1になる確率
表記 Pi=σ(w0+w1Xi1+・・・+wmXim)
数式 P(Y=1|X) = σ( w0 + w1X1)
P(Y=1|X):説明変数Xが与えられた時にY=1になる確率
w0:切片 ← 未知のため学習で決める
w1:回帰係数 ← 未知のため学習で決める
X1:説明変数 ← 既知の入力データ
データYは確率が0.5以上ならば1、0.5未満なら0と予測
- Q.シグモイド関数においてx=0.5の場合の「微分値」はいくらになるか下記の選択肢より一つ選べ。
選択肢
1. 0.265
2. 0.235
3. 0.6
4. 0.125 - A. 正解は2.の「0.235」

シグモイド関数におけるx=0.5の場合の「微分値」を暗算で解くのは無理だよ・・・

この問題は暗算をしなくても解けるよ!
理由は次のとおり。
- 連鎖率を思い出して欲しい。シグモイド関数の微分値はシグモイド関数で表すことができたよね。
δσ(x)/δx = σ(x)(1ーσ(x)) ← 連鎖率 - x=0の時、勾配の値が最大値をとるよ。
δσ(x)/δx = σ(x)(1ーσ(x))
=0.5×(1ー0.5)
=0.25
微分値は必ず0.25以下になるから、上記の選択肢のうち「1」,「3」は不正解と分かよ。
また、選択肢4について微分値が0.125になるためには、上記「連鎖率」の計算からx=1.7~1.8になりx≠0.5と予想ができるから選択肢4も間違いだと分かる。
よって、選択肢2が正解と分かる。

パラメータの推定(最尤法)
- 世の中には様々な確率分布が存在する
・正規分布、t分布、ガンマ分布、一様分布、ディリクレ分布・・・
・ロジスティック回帰モデル→ベルヌーイ分布を利用
- ベルヌーイ分布
・数学において、確率pで1、確率1-pで0をとる離散確率分布
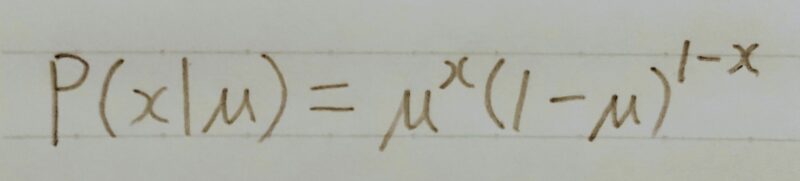

・例:コイントス
・裏と表が出る割合が等しくなくとも扱える
・「生成されるデータ」は分布のパラメータによって
異なる(この場合は確率p)
Y~ Be(p) P(y) = py(1ーp)1-y
ベルヌーイ分布に Y=0とY=1になる
従う確率変数Y 確率をまとめて表現
- ベルヌーイ分布のパラメータの推定:
ある分布を考えた時、そのパラメータ(既知)によって、生成されるデータは変化する。 - 最尤推定:
データからそのデータを生成したであろう尤(もっと)もらしい分布(パラメータ)を推定したい 。 - 同時確率
・あるデータが得られた時、それが同時に得られる確率
※あるデータは同じ分布からサンプルされていると仮定
・確率変数が独立であることを仮定すると、それぞれの確率の掛け算となる。
- 尤度関数:
パラメータθを変数としてみたときの関数 - 最尤推定:
データは固定し、パラメータを変化させる尤度関数を最大化するようなパラメータを選ぶ推定方法
※一般的に学習するデータ数が増えれば増えるほど、よい推定となる - 最尤推定量:
パラメータθに従う分布の密度関数をf(x;θ)とする。
尤度関数をL(x;θ)とすると、L(θ;x)を最大にするような推定量θ
例題1
Q.コインを8回投げたら「表、裏、表、裏、表、表、裏、裏」という結果になった。表が出る確率をθとすると、尤度関数はどう表現できるか?
A.θ4(1-θ)4
- ロジスティック回帰モデルの最尤推定
・確率pはシグモイド関数となるため、推定するパラメータは重みパラメータ
・(x1,y1),(x2,y2),・・・,(xn,yn)を生成するに至った尤もらしいパラメータを探す尤度関数Eを最大とするパラメータを探索
・最尤推定量は結果のみを利用 - 尤度関数を最大とするパラメータを探す(推定)
・対数をとると微分の計算が簡単
同時確率の積が和に変換可能
指数が積の演算に変換可能
・「対数尤度関数」が最大になる点=「尤度関数」が最大になる点
対数関数は単調増加
・「尤度関数にマイナスをかけたものを最小化」し、「最小二乗法の最小化」と合わせる。
E(w0,w1,・・・,wm) = -logL(wo,w1,・・・,wm)
=-Σ{yilogpi+(1-yi)log(1-pi)}
上式は「softmax_cross_entropy(ソフトマックスクロスエントロピー)」 - L2正則化(リッジ回帰)を適用できる
例題1
Q.コインを8回投げたら「表、裏、表、裏、表、表、裏、裏」という結果になった。表が出る確率をθとすると、尤度関数はどう表現できるか?
A.θ4(1-θ)4
例題2
Q.例題1の対数尤度関数はどのように表現できるか?
A.4logθ+4log(1ーθ)
- 反復学習によりパラメータを逐次的に更新するアプローチの一つ
- μは学習率と呼ばれるハイパーパラメータでモデルのパラメータの収束しやすさを調整

なぜ勾配降下法が必要なの?

それは次の理由からだよ!
- 勾配降下法(Gradient descent)が必要な理由
・[線形回帰モデル(最小二乗法)]→ MSE(平均二乗誤差)のパラメータに関する微分が0になる値を解析的に求めることが可能
・[ロジスティック回帰モデル(最尤法)]→対数尤度関数をパラメータで微分して0になる値を求める必要があるが、解析的にこの値を求めることは困難。
w(k+1) = wk – μδE(w)/δw - 「対数尤度関数」を係数とバイアスに関して微分
δE(w)/δw = Σ (δEi(w)/δpi)(δpi/δw)
= -Σ(yi-pi)xi
・パラメータが更新されなくなった場合、それは勾配が0になったということ。少なくとも反復学習で探索した範囲では最適な解が求められたことになる。
w(k+1) = w(k) + μΣ(yi-pi)xi - 勾配降下法では、パラメータを更新するのにN個全てのデータに対する和を求める必要がある。
・nが巨大になった時にデータをオンメモリに載せる容量が足りない、計算時間が莫大になるなどの問題がある。
・確率的勾配降下法(SGD)を利用して解決
- データを一つずつランダムに(「確率的」に)選んでパラメータを更新
- 勾配降下法でパラメータを1回更新するのと同じ計算量でパラメータをn回更新できるので効率よく最適な解を探索可能
w(k+1) = wk + μ(yi-pi)xi
Pi:正解値 - バッチ最急降下法
例題1
Q.コインを8回投げたら「表、裏、表、裏、表、表、裏、裏」という結果になった。表が出る確率をθとすると、尤度関数はどう表現できるか?
A.θ4(1-θ)4
例題2
Q.例題1の対数尤度関数はどのように表現できるか?
A.4logθ + 4log(1ーθ)
例題3
Q.例題2の対数尤度関数をθについて偏微分するとどのように表現できるか?
A.4/θ ー 4/(1ーθ)
- 例題1
Q.コインを8回投げたら「表、裏、表、裏、表、表、裏、裏」という結果になった。表が出る確率をθとすると、尤度関数はどう表現できるか?
A.θ4(1-θ)4 - 例題2
Q.例題1の対数尤度関数はどのように表現できるか?
A.4logθ + 4log(1ーθ) - 例題3
Q.例題2の対数尤度関数をθについて偏微分するとどのように表現できるか?
A.4/θ ー 4/(1ーθ) - 例題4
Q.例題3の最尤推定量はいくらか?
A.最尤推定量とは対数尤度関数が最大のときのθであるから、下式を偏微分した値が0(=グラフの傾きが0)のときのθを求める。
4/θ ー 4/(1ーθ) = 0
θ = 0.5 ← 表が出た回数/(表が出た回数+裏が出た回数) - 例題5
Q.表が出る確率3/4、裏が出る確率1/4の細工されたコインがある。このコインを7回投げたところ「表、表、裏、表、裏、表、裏」となった。コインの表の出る確率をθとするとθの最尤推定量はいくつか?
A.最尤推定量は「表が出た回数/(表が出た回数+裏が出た回数)」で算出できるから、
最尤推定量=4/7 ← 最尤推定量は結果のみを利用
モデルの評価
- 学習済みの「ロジスティック回帰モデル」の性能を測る指標
- 各検証データに対するモデルの予測結果を4つの観点(表)で分類し、それぞれに当てはまる予測結果の個数をまとめた表
①TP:True Positive
Positive(陽)と予測した結果がTrue(正しい)の場合
②FP:False Positive
Positive(陽)と予測した結果がFalse(間違い)の場合
異常な人を間違えて正常と判断してしまう。
③TN:True Negative
Negative(陰)と予測した結果がTrue(正しい)の場合
④FN:False Negative
Negative(陰)と予測した結果がFalse(間違い)の場合
正常な人を間違えて異常と判断してしまう。 - 混同行列の表
| 実際の値\予測値 | 陽 (Positive) | 陰 (Negative) | |
|---|---|---|---|
| 真 (Positive) | 真陽性 TP(True Positive) | 偽陰性 FN(False Negative) | 再現率 (Recall) |
| 偽 (Negative) | 偽陽性 FP(False Positive) | 真陰性 TN(True Negative) | |
| 適合率 (Precision) | 正解率 (Correct answer rate) |
- 正解率がよく使われる
- 正解率=正解した数/予測対象となった全データ数
- 例)メールのスパム分類
スパム数が80件・普通のメールが20件であった場合全てをスパムとする分類器の正解率は80%となる。
- 分類したいクラスにはそれぞれ偏りがあることが多い
この場合、単純な正解率はあまり意味をなさないことがほとんど - 本当に検知したい脅威が見えなくなる。
- 例:表情から怪しい人物を検知する動画分析ソリューション
全スライドの正解率が適当ではない例→再現率(Recall)や適合率(Precision)を使って評価
- 「本当にPositiveなもの」の中からPositiveと予測できる割合
TP/(TP+FN) - 「誤り(False Positive)が多少多くても抜け漏れが少ない」予測をしたい際に利用
(本当にNegativeなものをPositiveとしてしまう事象については考えていない) - 使用例:
病気の検診で「陽性であるものを陰性と誤診(FalseNegative)」としてしまうのを避けたい。「陰性を陽性であると誤診(FalsePositive)」とするものが少し増えたとしても再検査すればよいい。
- 「Positiveと予測」したものの中で本当にPositiveである割合
TP/(TP+FP) - 「見逃し(False Negative) が多くてもより正確な」予測をしたい際に利用
(本当にPositiveなものをNegativeとしてしまう事象についは考えていない。) - 使用例:
「重要なメールをスパムメールと誤判別」されるより「スパムと予測したものが確実にスパム」である方が便利。スパムメール検出できなくても(FalseNegative)、自分でやればいい。
- 不均衡データに対して用いられる。
※不均衡データとはTP、FP、TN、FNに偏りがあるデータ - 理想的には再現率(Recall)と適合率(Precision)はどちらも高いモデルがいいモデルだが、両者はトレードオフの関係
- 再現率(Recall)と適合率(Precision)の調和平均
F1値は再現率(Recall)と適合率(Precision)のバランスを示している。高ければ高いほどRecallとPrecisionがともに高くなる。
※True Negativeの情報は不要 - 〈欠点〉ラベルの付け方により値が異なる
例)罹患している人を「陽性」とするか「陰性」とするかでF1値が変わってしまう。
- 不均衡なデータに対して用いられる。
※不均衡データとはTP、FP、TN、FNに偏りがあるデータ - F1値(F1ーscore)の欠点を解消したもの。
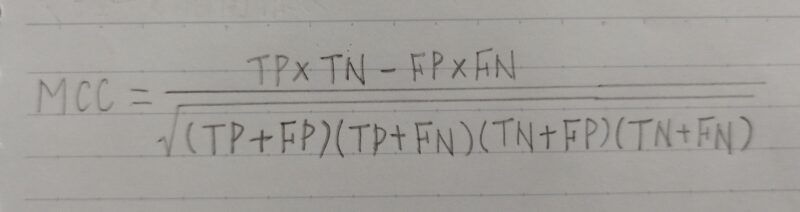
- MCCは -1~+1 の相関係数値である。
+1:完全予測
0:平均ランダム予測
ー1:係数逆予測 - MCCが1に近い程、分類器としての性能は高い
- 精度、再現率以外の評価指標
- ROC曲線(Receiver Operatorating Characteristic curve)とは・・・
横軸にFalse Positive Rate(FPR)、縦軸にTPR(True Positive Rate)をとったグラフ
TPR=TP/(TP+FN)
FPR=FP/(FP+TN) - 良いモデルの条件:FPRが小さい時にTPRが大きい
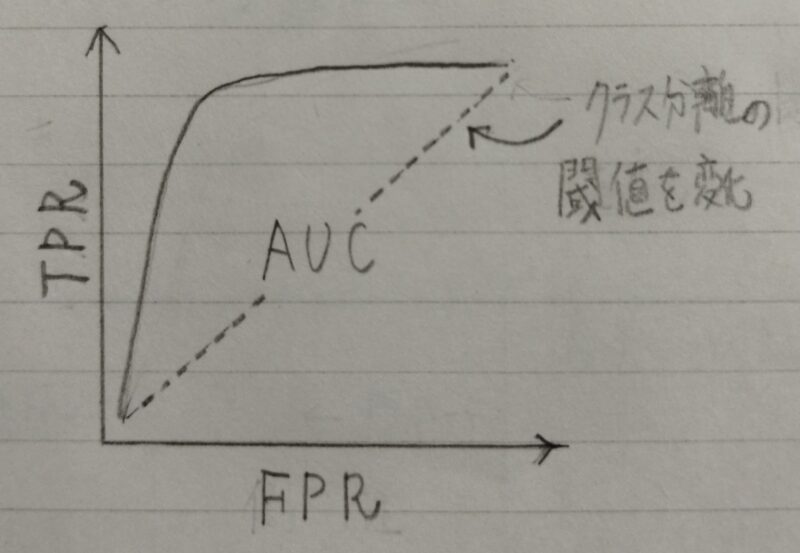
補足)AUC(Area Under an ROC curve):ROC曲線の横軸と縦軸に囲まれた
部分の面積
実装演習
- 設定
〇タイタニックの乗客データを利用しロジスティック回帰モデルを作成
〇特徴量抽出をしてみる - 課題
〇年齢が30歳で男の乗客は生き残れるか?
まとめ
最後まで読んで頂きありがとうございます。
皆様のキャリアアップを応援しています!!

コメント