- 「機械学習」について学びたいけど理解できるか不安・・・
- 「機械学習」についてどこから学んでいいか分からない?
- 「機械学習」を体系的に教えて!
「人工知能(AI:Artificial intelligence)」を勉強する際、その基礎である「機械学習」の考え方を理解していないため人工知能が理解できないケースは非常に多いです。
私は過去に基本情報技術者試験(旧:第二種情報処理技術者試験)に合格し、また2年程前に「一般社団法人 日本ディープラーニング協会」が主催の「G検定試験」に合格しました。現在、「E資格」にチャレンジ中ですが3回不合格になり、この経験から学習の要点について学ぶ機会がありました。
そこでこの記事では、「機械学習」のうち「線形回帰モデル」についてポイントを解説します。
この記事を参考にして「線形回帰モデル」が理解できれば、E資格に合格できるはずです。
アウトライン
- コンピュータプログラムは、タスクT(アプリケーションにさせたいこと)を性能指標Pで測定し、その性能が経験E(データ)により改善される場合、タスクTおよび性能指標Pに関して経験Eから学習すると言われている(トム・ミッチェル1997)
- 人がプログラムするのは認識の仕方ではなく学習の仕方(数学で記述)
- パラメータの推定問題:最小二乗法・尤度最大化
データ形式の説明
- 回帰問題
〇ある入力(離散あるいは連続値)から出力(連続値)を予測する問題
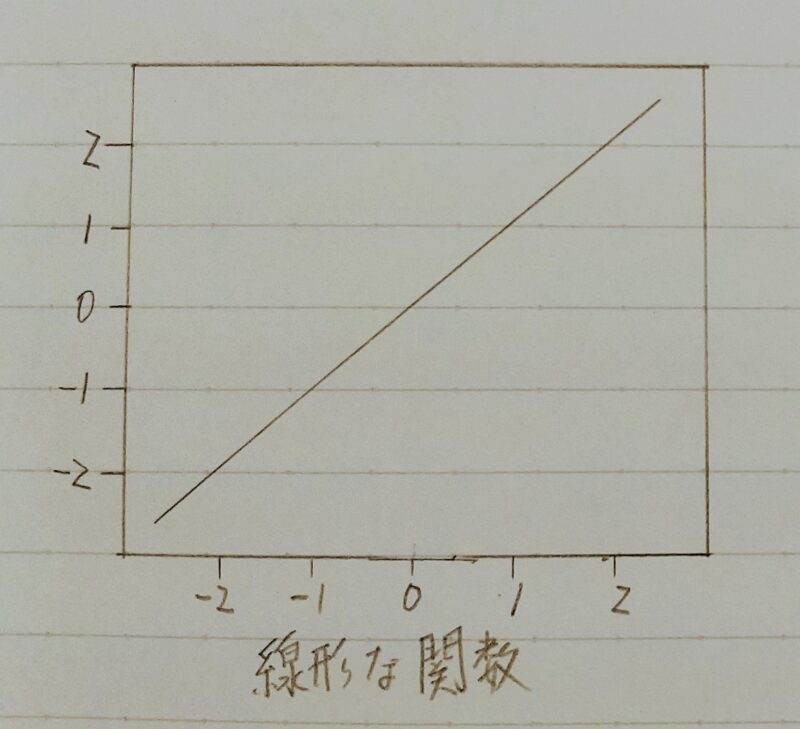
■直線で予測→線形回帰
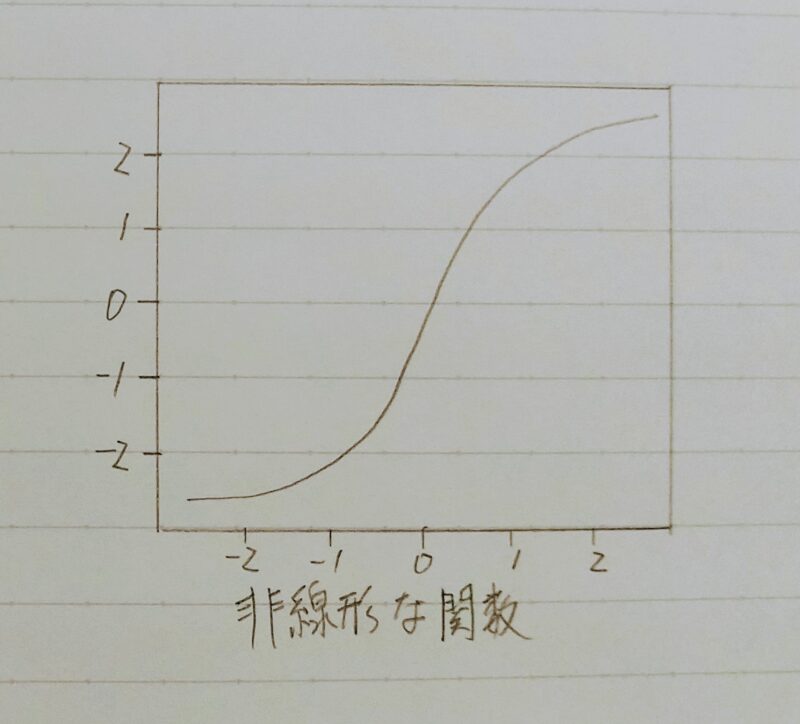
■曲線で予測→非線形回帰 - 回帰で扱うデータ
〇入力(各要素を説明変数または特徴量と呼ぶ)
■m次元のベクトル(m=1の場合はスカラ)
〇出力(目的変数)
■スカラー値(目的変数)
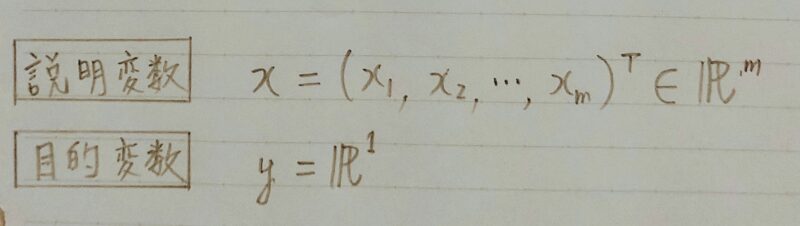
線形回帰モデルの説明
- 回帰問題を解くための機械学習モデルの一つ
- 教師あり学習(教師データから学習)
- 入力とm次元パラメータの線形結合を出力するモデル
慣例として予測値にはハットを付ける(正解データとは異なる)
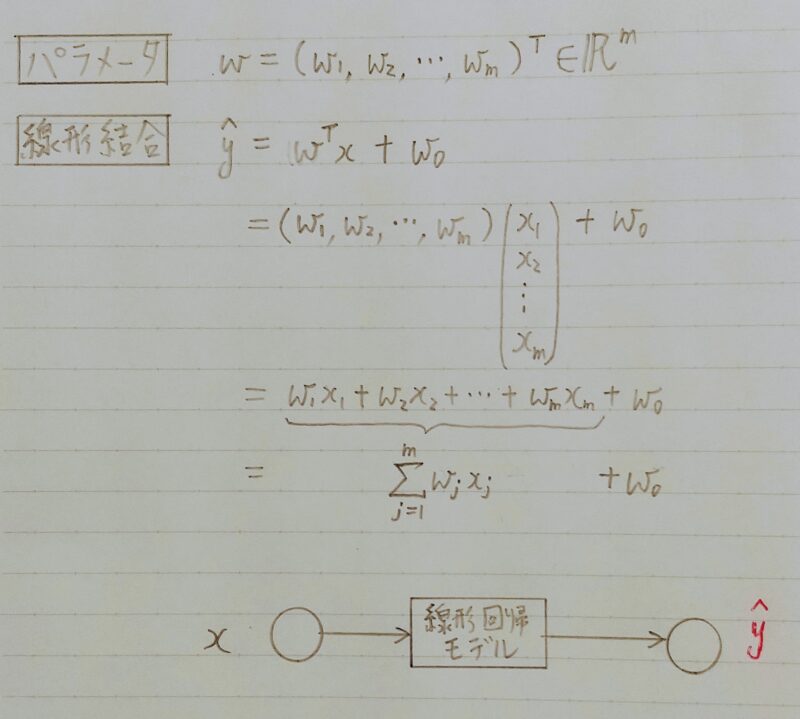
- 入力ベクトルと未知のパラメータの各要素を掛け算し足し合わせたもの
- 入力ベクトルと線形結合に加え、切片も足し合わせる
- (入力のベクトルが多次元でも)出力は1次元(スカラ)となる
パラメータの推定
- モデルに含まれる推定すべき未知のパラメータ
- 特徴量が予測値に対してどのように影響を与えるかを決定する重みの集合
■正の(負の)重みをつける場合、その特徴量の値を増加させると、予測の値が増加(減少)
■重みが大きければ(0であれば)、その特徴量は予測に大きな影響力を持つ(全く影響しない) - 切片
■y軸との交点を表す
パラメータは未知 → 最小二乗法により推定
| 説明変数 | 1次元の場合(m=1) | 多次元の場合(m>1) |
|---|---|---|
| モデル | 単回帰モデル | 線形重回帰モデル |
| データへの仮定 | データは回帰直線に誤差が加わり観測 されていると仮定 | データは回帰曲面に誤差が加わり観測されていると仮定 |
| 方程式 | それぞれのデータをモデル式へ当てはめるとn個の式が導出される |
- 学習用データ:機械学習モデルの学習に利用するデータ
- 検証用データ:学習済みモデルの精度を検証するためのデータ

なぜデータを分割するの?

次の2つの理由からだよ!!
- モデルの汎化性能(Generalization)を測定するため
汎化性能:データへの当てはまりの良さではなく、未知のデータに対してどれくらい精度が高いかの性能
線形回帰モデルのパラメータは最小二乗法で推定
- 平均二乗誤差(=残差平方和)(MSE:Mean Square Error)
・データとモデル出力の二乗誤差の和
■小さいほど直線とデータの距離が近い
・パラメータのみに依存する関数
■データは既知の値でパラメータのみ未知 - 最小二乗法
・学習データの「平均二乗誤差」を最小とするパラメータを検索
・学習データの「平均二乗誤差」の最小化は、その勾配が0になる点を求めれば良い - [topic]最尤法による回帰係数の推定
・誤差を正規分布に従う確率変数を仮定し尤度関数の最大化を利用した推定も可能
・線形回帰の場合には、「最尤法による解=最小二乗法の解」
Q.下記の訓練データが与えられた時、Y=aX+bと仮定すると、回帰係数a,bの値について最も近いものを下記の選択肢より選べ。
| X | Y |
|---|---|
| -1.0 | 1.0 |
| 0.5 | 0.15 |
| 1.0 | 0.1 |
| 2.0 | -0.5 |
1.a=0.9,b=-0.5
2.a=-0.5,b=0.5
3.a=-0.5,b=1.0
4.a=0.5,b=-0.6
A.正解は2

回帰係数を計算で解くの面倒くさいな・・・

わざわざ回帰係数を計算で求めなくても解答できるよ! 理由は次のとおり。
- まずaはY=aX+bの「傾き」を表し、訓練データをプロットすると傾きは「負」であることが分かるよ。
よって、選択肢1と4は不正解。 - つぎにbはY=aX+bの「切片」を表す。切片とはX=0のときのYの値である。訓練データから、X=-0.1のときY=1.0、X=0.5のときY=0.15であるからX=0のときY≠1.0と推測できるよ。よって、選択肢3も不正解と分かるよ。
モデルの評価(ホールドアウト法、交差検証法)
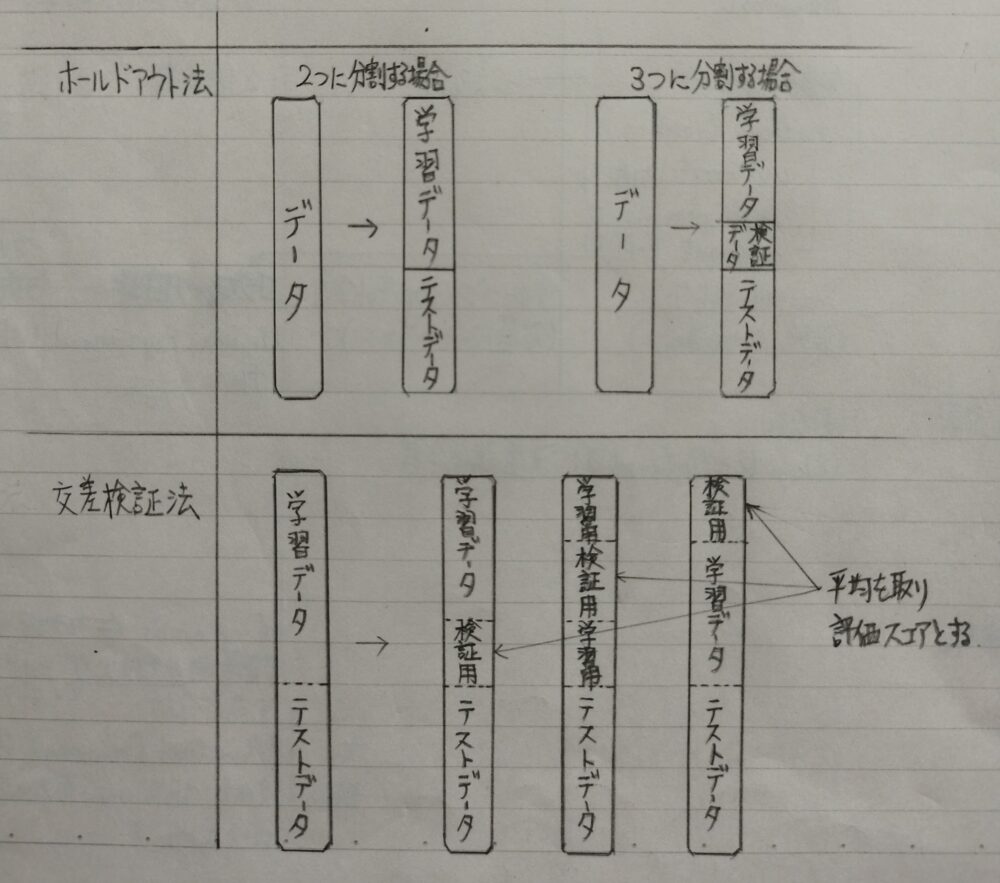
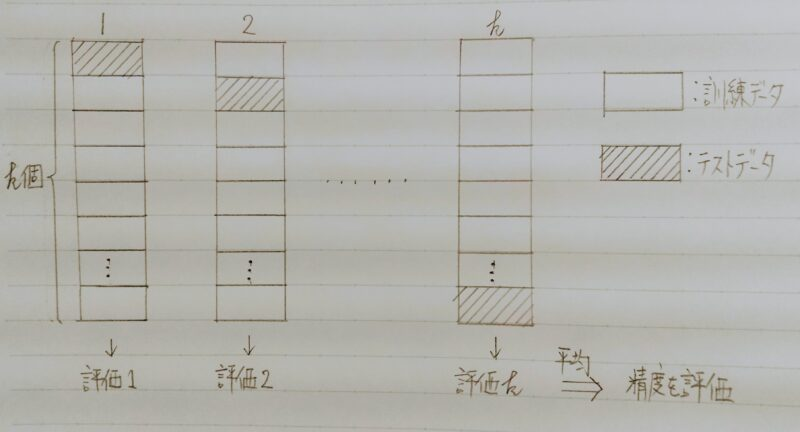
- データをk個の重複しない集合に分割し、そのうちの1個をテストデータ、残りのk-1 個を訓練データとして、推定値を得る。
- 同様にk 個に分割された集合のそれぞれが1回ずつテスト事例となるよう合計k回、推定値を計算する。
- 上記を行い得られたk回の結果を平均して1つの推定値を得る。さらに、標本の分割から始まる一連の操作を複数回繰り返して平均を取る場合もある。
| ホールドアウト法 (holdーout method) | 交差検証法 (cross-validation method) | |
|---|---|---|
| 計算コスト | 小 (大規模データに対して) | 大 (大規模データに対して) |
| 評価結果の信頼性 | 低 (手元のデータ数が少ない場合) | 高 (手元のデータ数が少ない場合) |
実装演習
pandasとnumpyの紹介
利用するライブラリの説明
Pandas:Excelのような2次元のテーブルを大勝したデータ解析を支援する機能を提供するライブラリ。DataFrameがpandasのメインとなるデータ構造で二次元のテーブルを表す。
Numpy:値計算を効率的に行うための拡張モジュールである。効率的な数値計算を行うための型付きの多次元配列(例えばベクトルや行列などを表現できる)のサポートをPythonに加えるとともに、それらを操作するための大規模な高水準の数学関数ライブラリを提供する。統計処理、機械学習を行う際に共によく利用
scikit-learnの紹介
Scikit-learn:PythonのOpen-Sourceライブラリ特徴:様々な回帰・分類・クラスタリングアルゴリズムが実装されており、Pythonの数値計算ライブラリのNumPyとSciPyとやりとりするように設計されている。(先ほどのPandasはデータ表示・解析に利用)
住宅価格予測
●設定
〇ボストンの住宅データセットを線形回帰モデルで分析
〇適切な査定結果が必要
■高すぎても安すぎても会社に損害がある
●課題
〇部屋数が4で犯罪率が0.3の物件はいくらになるか?
まとめ
最後まで読んで頂きありがとうございます。
皆様のキャリアアップを応援しています!!

コメント